Aufgabe 4083
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Angewandte Mathematik
Quelle: BHS Matura vom 09. Mai 2018 - Teil-B Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Smartphones - Aufgabe B_079
Der Akku eines Smartphones entlädt sich aufgrund von Hintergrundanwendungen auch dann, wenn das Gerät nicht aktiv benutzt wird.
Teil a
Für ein bestimmtes Smartphone wird die zeitliche Entwicklung des Akku-Ladestands in Prozent beobachtet. Zur Zeit t = 0 ist der Akku vollständig aufgeladen.
| Zeit t in Stunden | Akku-Ladestand in Prozent |
| 0 | 100 |
| 3 | 94 |
| 6 | 81 |
| 10 | 71 |
| 18 | 43 |
Die zeitliche Entwicklung des Akku-Ladestands in Prozent soll beschrieben werden.
1. Teilaufgabe - Bearbeitungszeit 5:40
Ermitteln Sie eine Gleichung der zugehörigen linearen Regressionsfunktion.
[1 Punkt]
Bei einem Akku-Ladestand von 15 % sollte das Smartphone wieder ans Stromnetz angeschlossen werden.
2. Teilaufgabe - Bearbeitungszeit 5:40
Berechnen Sie, wie viele Stunden nach dem vollständigen Aufladen dies gemäß diesem linearen Regressionsmodell gemäß Teil a der Fall ist.
[1 Punkt]
Lösungsweg
1. Teilaufgabe:
Die Regressionsgerade ist die bestmögliche Gerade, die man in einem Streudiagramm durch alle Daten legen kann, sodass alle Datenpunkte von der Geraden in Summe den kleinsten Abstand haben.
Wir ermitteln die Regressionsgerade mittels Technologieeinsatz:
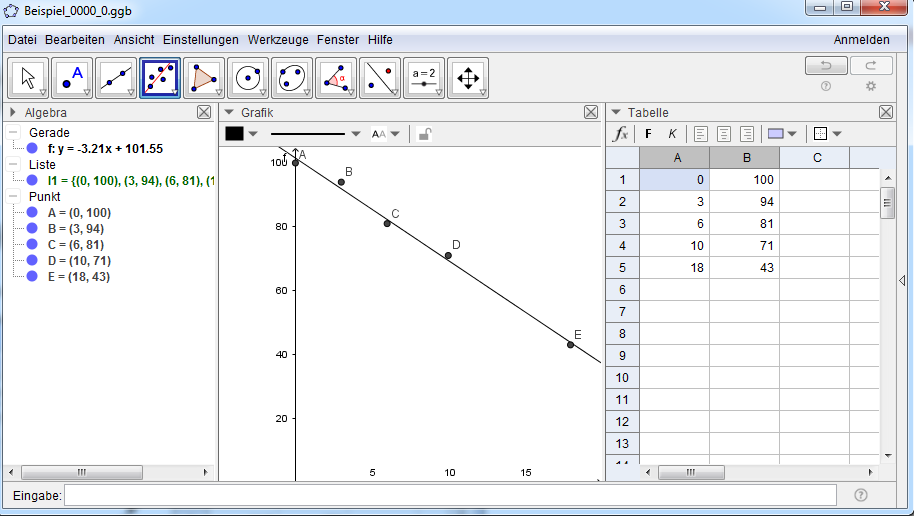
GeoGebra:
- Tabellen + Grafik + Algebra Ansicht aktivieren
- Ansicht → Tabelle → die 8 Datensätze gemäß Angabe eingeben
- alle Datensätze mit Rechteck auswählen → rechte Maustaste → Erzeugen → Liste von Punkten
- Bearbeiten → Eigenschaften → Grundeinstellungen →
- x-Achse: -5 .. 20 und y-Achse: 0 .. 105 einstellen
- allenfalls das Koordinatengitter ausblenden
- Grafik-Ansicht → 4. Icon → Regressionsgerade
- Algebra-Ansicht: Die Gleichung der Regressionsgeraden ist wie folgt ablesbar:
\(L\left( t \right) = - 3,21 \cdot t + 101,55\)
- t ... Zeit in h
- L(t) ... Akku-Ladestand zur Zeit t in %
2. Teilaufgabe:
Wir setzen L(t)=15 in die Regressionsgerade aus Teil a ein und machen t explizit:
\(\begin{array}{l} L\left( t \right) = - 3,210 \cdot t + 101,554\\ \\ 15 = - 3,210 \cdot t + 101,554\\ 3,210 \cdot t = 101,554 - 15\\ \\ t = \dfrac{{86,554}}{{3,210}} \approx 26,9 \end{array}\)
→ Nach etwa 27 Stunden sollte das Smartphone wieder ans Stromnetz angeschlossen werden.
Ergebnis
Die richtige Lösung lautet:
1. Teilaufgabe:
\(L\left( t \right) = - 3,21 \cdot t + 101,55\)
2. Teilaufgabe:
Nach etwa 27 Stunden sollte das Smartphone wieder ans Stromnetz angeschlossen werden.
Lösungsschlüssel:
1. Teilaufgabe:
1 × B1: Für das richtige Ermitteln der Gleichung der Regressionsfunktion (KA)
2. Teilaufgabe:
1 × B2: Für die richtige Berechnung des Zeitpunkts (KB)