Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 1. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Bei Solarthermie-Anlagen wird die Sonnenstrahlung von sogenannten Solarmodulen in Wärme umgewandelt. Diese Wärme kann beispielsweise zur Warmwassererzeugung oder zur Heizung von Gebäuden verwendet werden.
Teil a
Ein Solarmodul einer Solarthermie-Anlage mit der Lange l schließt mit dem waagrechten Erdboden den Winkel φ ein. Dieser Winkel φ wird durch eine Stütze mit variabler Lange s so verändert, dass das Solarmodul mit den Sonnenstrahlen einen rechten Winkel einschließt. Die Sonnenstrahlen treffen unter dem Winkel ε auf den Erdboden auf.
Die Situation ist in der nachstehenden Abbildung modellhaft dargestellt.
1. Teilaufgabe - Bearbeitungszeit 05:40
Geben Sie eine Formel an, mit der s unter Verwendung von l und ε berechnet werden kann.
s =
Das oben abgebildete Solarmodul hat die Lange l = 1 666 mm. Bei diesem Solarmodul nimmt der Winkel ε im Laufe eines bestimmten Tages Werte von 14° bis 65° an.
2. Teilaufgabe - Bearbeitungszeit 05:40
Geben Sie den maximalen Wert von s in mm an.
maths2mind
Kreditkarte? - Braucht man nicht!
Kostenpflichtige Pakete? Gibt es nicht!
Nach der Prüfung genießt du mit dem gesparten Geld deinen Erfolg
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 1. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Bei Solarthermie-Anlagen wird die Sonnenstrahlung von sogenannten Solarmodulen in Wärme umgewandelt. Diese Wärme kann beispielsweise zur Warmwassererzeugung oder zur Heizung von Gebäuden verwendet werden.
Teil b
Die Leistung einer bestimmten Solarthermie-Anlage an einem wolkenfreien Tag wird durch die Funktion P modelliert. Dabei gilt:
\(P\left( t \right) = 0,0136 \cdot {a^3} \cdot {t^4} - 0,272 \cdot {a^2} \cdot {t^3} + 1,36 \cdot a \cdot {t^2}\)
| t | Zeit in h, die seit dem Sonnenaufgang (t = 0) vergangen ist |
| P(t) | Leistung in kW zur Zeit t |
| a | Parameter |
Beim Sonnenaufgang und beim Sonnenuntergang beträgt die Leistung der Solarthermie-Anlage 0 kW. Zwischen Sonnenaufgang und Sonnenuntergang nimmt die Funktion P positive Werte an.
1. Teilaufgabe - Bearbeitungszeit 05:40
Ermitteln Sie für diese Solarthermie-Anlage den Wert des Parameters a für einen bestimmten wolkenfreien Tag, an dem die Sonne um 7:08 Uhr aufgeht und um 18:38 Uhr untergeht.
Die Arbeit, die von der Solarthermie-Anlage zwischen den zwei Zeitpunkten t1 und t2 verrichtet wird, ist
\(\int\limits_{{t_1}}^{{t_2}} {P\left( t \right)} \,dt\)
2. Teilaufgabe - Bearbeitungszeit 05:40
Berechnen Sie die an diesem Tag von der Solarthermie-Anlage verrichtete Arbeit (in kWh).
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 2. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Teil a
Der Benzinverbrauch eines bestimmten Kleinwagens kann in Abhängigkeit von der Geschwindigkeit modellhaft durch die Funktion B beschrieben werden.
\({B_v} = 0,000483 \cdot {v^2} - 0,0326 \cdot v + 2,1714 + \dfrac{{66}}{v}{\rm{ mit }}20 < v < 150\)
| v |
Geschwindigkeit in km/h |
| B(v) |
Benzinverbrauch in Litern pro 100 km (L/100 km) bei der Geschwindigkeit v |
1. Teilaufgabe - Bearbeitungszeit 05:40
Berechnen Sie, um wie viel Prozent der Benzinverbrauch bei einer Geschwindigkeit von 90 km/h höher als bei einer Geschwindigkeit von 70 km/h ist.
Der Benzinverbrauch bei einer Geschwindigkeit von 40 km/h ist um 25 % geringer als der Benzinverbrauch bei einer Geschwindigkeit v1 mit 20 < v1 < 40.
2. Teilaufgabe - Bearbeitungszeit 05:40
Ermitteln Sie die Geschwindigkeit v1.
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 2. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Teil b
Für hohe Geschwindigkeiten soll die Funktion B durch eine lineare Funktion f mit
\(f\left( v \right) = k \cdot v + d{\text{ mit }}k,d \in {\Bbb R}\)
angenähert werden, sodass gilt:
1. Teilaufgabe - Bearbeitungszeit 05:40
Ermitteln Sie einen Funktionsterm f(v) der Funktion f.
Diese Näherung kann verwendet werden, wenn die Abweichung zwischen den Funktionswerten von f und B höchstens 0,3 L/100 km beträgt.
2. Teilaufgabe - Bearbeitungszeit 05:40
Geben Sie das größtmögliche Intervall für die Geschwindigkeit an, in dem die Funktion f als Näherung verwendet werden kann.
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 3. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Afrika hatte Ende 2018 eine Bevölkerung von ca. 1,3 Milliarden Menschen und verzeichnet derzeit das stärkste Bevölkerungswachstum aller Kontinente.
Teil a
Die nachstehende Abbildung zeigt die Alterspyramide der afrikanischen Bevölkerung im Kalenderjahr 2018. Der Alterspyramide ist z. B. zu entnehmen, dass im Kalenderjahr 2018 galt: 4,5 % der afrikanischen Bevölkerung sind Männer mit einem Lebensalter von 20 bis 24 Jahren und 4,4 % der afrikanischen Bevölkerung sind Frauen mit einem Lebensalter von 20 bis 24 Jahren. Unter Lebensalter versteht man die Anzahl vollendeter Lebensjahre.
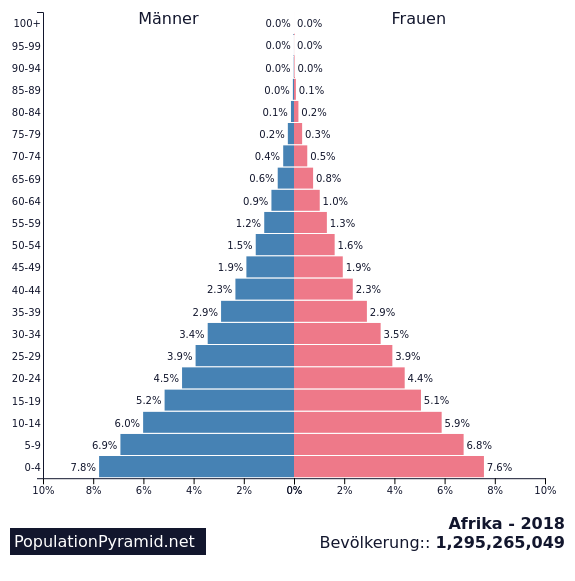
Datenquelle: https://www.populationpyramid.net/de/afrika/2018 [07.08.2023].
Nehmen Sie modellhaft an, dass in jeder Altersklasse die einzelnen Lebensalter gleich häufig auftreten.
1. Teilaufgabe - Bearbeitungszeit 05:40
Bestimmen Sie anhand der Alterspyramide den Median m des Lebensalters der afrikanischen Bevölkerung im Kalenderjahr 2018.
2. Teilaufgabe - Bearbeitungszeit 05:40
Geben Sie die Anzahl an Afrikanerinnen und Afrikanern an, die im Kalenderjahr 2018 junger als m Jahre waren.
maths2mind
Kreditkarte? - Braucht man nicht!
Kostenpflichtige Pakete? Gibt es nicht!
Nach der Prüfung genießt du mit dem gesparten Geld deinen Erfolg
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 3. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Afrika hatte Ende 2018 eine Bevölkerung von ca. 1,3 Milliarden Menschen und verzeichnet derzeit das stärkste Bevölkerungswachstum aller Kontinente.
Teil b
Die nachstehende Abbildung zeigt die prognostizierte Bevölkerungsentwicklung (Angaben in Millionen) im Zeitraum von 2010 bis 2050 in ausgewählten afrikanischen Ländern.
Abbildung fehlt
Datenquelle: https://de.statista.com/statistik/daten/studie/159204/umfrage/prognose-… [10.05.2019].
1. Teilaufgabe - Bearbeitungszeit 05:40
Geben Sie von den zehn angeführten Ländern dasjenige Land an, das laut Prognose im Zeitraum von 2010 bis 2050 am stärksten zum absoluten Bevölkerungswachstum in Afrika beitragen wird.
2. Teilaufgabe - Bearbeitungszeit 05:40
Geben Sie von den zehn angeführten Ländern dasjenige Land an, in dem laut Prognose im Zeitraum von 2010 bis 2050 das stärkste relative Bevölkerungswachstum erfolgt.
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 3. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Afrika hatte Ende 2018 eine Bevölkerung von ca. 1,3 Milliarden Menschen und verzeichnet derzeit das stärkste Bevölkerungswachstum aller Kontinente.
Teil c
Die nachstehende Tabelle zeigt die Bevölkerungsentwicklung in Nigeria im Zeitraum von 1980 bis 2010.
| Kalenderjahr | 1980 | 1990 | 2000 | 2010 |
| Bevölkerungszahl in Millionen | 73,5 | 95,3 | 122,4 | 158,6 |
1. Teilaufgabe - Bearbeitungszeit 05:40
Zeigen Sie anhand der Tabelle, dass die Bevölkerungszahl im Zeitraum von 1980 bis 2010 annähernd exponentiell zugenommen hat.
Nehmen Sie an, dass die Bevölkerungszahl von Nigeria weiterhin in dieser Art exponentiell wachsen wird.
2. Teilaufgabe - Bearbeitungszeit 05:40
Geben Sie unter Verwendung der Daten aus den beiden Kalenderjahren 2000 und 2010 an, in welchem Kalenderjahr die Bevölkerungszahl Nigerias erstmals mehr als 360 Millionen betragen wird.
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 3. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Afrika hatte Ende 2018 eine Bevölkerung von ca. 1,3 Milliarden Menschen und verzeichnet derzeit das stärkste Bevölkerungswachstum aller Kontinente.
Teil d
Die nachstehende Tabelle zeigt, wie sich die durchschnittliche Lebenserwartung der afrikanischen Bevölkerung seit 1953 entwickelt hat.
| Kalenderjahr | durchschnittliche Lebenserwartung in Jahren |
| 1953 | 37,5 |
| 1958 | 40,0 |
| 1963 | 42,3 |
| 1968 | 44,4 |
| 1973 | 46,6 |
| 1978 | 48,7 |
| 1983 | 50,5 |
| 1988 | 51,7 |
| 1993 | 51,7 |
| 1998 | 52,3 |
| 2003 | 53,7 |
| 2008 | 57,0 |
| 2013 | 60,2 |
| 2018 | 62,4 |
1. Teilaufgabe - Bearbeitungszeit 05:40
Berechnen Sie die mittlere jährliche Zunahme k der durchschnittlichen Lebenserwartung im Zeitraum von 1953 bis 2018.
Es wird angenommen, dass die durchschnittliche Lebenserwartung in Afrika nach dem Kalenderjahr 2018 konstant pro Jahr um den berechneten Wert k zunimmt. Im Kalenderjahr 2018 betrug die durchschnittliche Lebenserwartung in Europa 78,5 Jahre.
2. Teilaufgabe - Bearbeitungszeit 05:40
Geben Sie an, in welchem Kalenderjahr die durchschnittliche Lebenserwartung in Afrika unter dieser Annahme den Wert für Europa im Kalenderjahr 2018 erreichen wurde.
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 4. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Beim Einlass in ein bestimmtes Stadion findet bei einer Veranstaltung eine maximal dreistufige Sicherheitskontrolle bei Personen statt, um mitgeführte Gegenstande zu kontrollieren und unzulässige Gegenstande zu erfassen. Liefert die erste Stufe dieser Sicherheitskontrolle kein eindeutiges Ergebnis, dann wird die zweite Stufe der Sicherheitskontrolle durchgeführt. Liegt dann noch immer kein eindeutiges Ergebnis vor, kommt die dritte Stufe der Sicherheitskontrolle zum Einsatz.
Teil a
Die erste und die zweite Stufe der Sicherheitskontrolle dauern jeweils 15 s, die dritte Stufe dauert 300 s. Ein eindeutiges Ergebnis liefert dabei die erste Stufe mit einer Wahrscheinlichkeit von 90 %, die zweite Stufe mit einer Wahrscheinlichkeit von 60 %.
Die Zufallsvariable X beschreibt die Dauer d (in s) der Sicherheitskontrolle bei einer Person. Wartezeiten, die eventuell auftreten können, werden nicht berücksichtigt.
1. Teilaufgabe - Bearbeitungszeit 05:40
Ergänzen Sie in der nachstehenden Tabelle die Wahrscheinlichkeitsverteilung der Zufallsvariablen X.
| d | |||
| P(X=d) |
2. Teilaufgabe - Bearbeitungszeit 05:40
Ermitteln Sie den Erwartungswert E(X).
maths2mind
Kreditkarte? - Braucht man nicht!
Kostenpflichtige Pakete? Gibt es nicht!
Nach der Prüfung genießt du mit dem gesparten Geld deinen Erfolg
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 4. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Beim Einlass in ein bestimmtes Stadion findet bei einer Veranstaltung eine maximal dreistufige Sicherheitskontrolle bei Personen statt, um mitgeführte Gegenstande zu kontrollieren und unzulässige Gegenstande zu erfassen. Liefert die erste Stufe dieser Sicherheitskontrolle kein eindeutiges Ergebnis, dann wird die zweite Stufe der Sicherheitskontrolle durchgeführt. Liegt dann noch immer kein eindeutiges Ergebnis vor, kommt die dritte Stufe der Sicherheitskontrolle zum Einsatz.
Teil b
Der Wert p gibt die Wahrscheinlichkeit an, dass eine Person einen unzulässigen Gegenstand mit sich führt. Die Wahrscheinlichkeit, dass von 2 zufällig und unabhängig voneinander ausgewählten Personen beide einen unzulässigen Gegenstand mit sich fuhren, beträgt 10 %.
1. Teilaufgabe - Bearbeitungszeit 05:40
Berechnen Sie die Wahrscheinlichkeit p.
2. Teilaufgabe - Bearbeitungszeit 05:40
Ermitteln Sie die Wahrscheinlichkeit, dass von 10 zufällig und unabhängig voneinander ausgewählten Personen mindestens 5 Personen einen unzulässigen Gegenstand mit sich führen.
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Mathematik
Quelle: AHS Matura vom 16. September 2020 - Teil-2-Aufgaben - 4. Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Beim Einlass in ein bestimmtes Stadion findet bei einer Veranstaltung eine maximal dreistufige Sicherheitskontrolle bei Personen statt, um mitgeführte Gegenstande zu kontrollieren und unzulässige Gegenstande zu erfassen. Liefert die erste Stufe dieser Sicherheitskontrolle kein eindeutiges Ergebnis, dann wird die zweite Stufe der Sicherheitskontrolle durchgeführt. Liegt dann noch immer kein eindeutiges Ergebnis vor, kommt die dritte Stufe der Sicherheitskontrolle zum Einsatz.
Teil c
Die momentane Änderungsrate der Anzahl der Personen im Stadion kann mithilfe der Funktion A mit
\(A\left( t \right) = a \cdot {t^2} + b \cdot t + c{\text{ mit a}}{\text{,b}}{\text{,c}} \in {\Bbb R}{\text{ und }}0 \leqslant t \leqslant 90\)
in Abhängigkeit von der Zeit t beschrieben werden, wobei zum Zeitpunkt t = 0 der Einlass ins Stadion beginnt.
| t | Zeit in Minuten |
| A(t) | Anzahl der Personen pro Minute |
Zum Zeitpunkt t = 0 kommt keine Person ins Stadion, 45 min nach Einlassbeginn kommen 15 Personen pro Minute ins Stadion. Zu diesem Zeitpunkt ist die momentane Änderungsrate der Anzahl der ins Stadion kommenden Personen pro Minute am größten.
1. Teilaufgabe - Bearbeitungszeit 05:40
Berechnen Sie die Werte von a, b und c.
2. Teilaufgabe - Bearbeitungszeit 05:40
Geben Sie die Anzahl der Personen an, die insgesamt bis zum Zeitpunkt t = 90 ins Stadion gekommen sind.