GeoGebra

Lektion 1: Grundlegende Bedienung von GeoGebra

In dieser Mikro-Lerneinheit verschaffen wir uns einen Überblick über die wesentlichen Bedienelemente von GeoGebra. Wir lernen die Hauptansichten kennen, die vier ansichtenspezifischen Werkzeugleisten, die Menüleiste, die beiden Eingabezeilen und die virtuelle Tastatur. Klicke die einzelnen Icons mal an und erfahre mehr über die vielfältigen Möglichkeiten des Programms.

Zuerst verschaffst du dir zuerst einen Überblick darüber, welche Aufgabenstellungen mit GeoGebra überhaupt gelöst werden können. Mit welcher Eingabe man dann eine konkrete Aufgabenstellung löst, weiß man - bei häufig wiederkehrenden Aufgabenstellungen - auswendig, oder - bei selteneren Aufgabenstellungen – schaut man in der Dokumentation nach. 

Die Hauptansichten

GeoGebra ist ein dynamisches Mathematikprogramm, welches bis zu 5 verschiedene Ansichten auf ein und dasselbe mathematische Objekt (z.B.: die Gleichung einer Geraden \(y = f(x) = k \cdot x + d\)) liefert. GeoGebra verbindet geometrischen Darstellungen („Grafik“) mit algebraische Ein- bzw. Ausgaben („Algebra“) und ermöglicht Parametervariationen mit Schiebereglern. Zusätzlich verfügt es über ein Computer Algebra System („CAS“), eine rudimentäre Tabellenkalkulation („Tabelle“) und ein Statistikmodul („Wahrscheinlichkeitsrechner“).

Bild

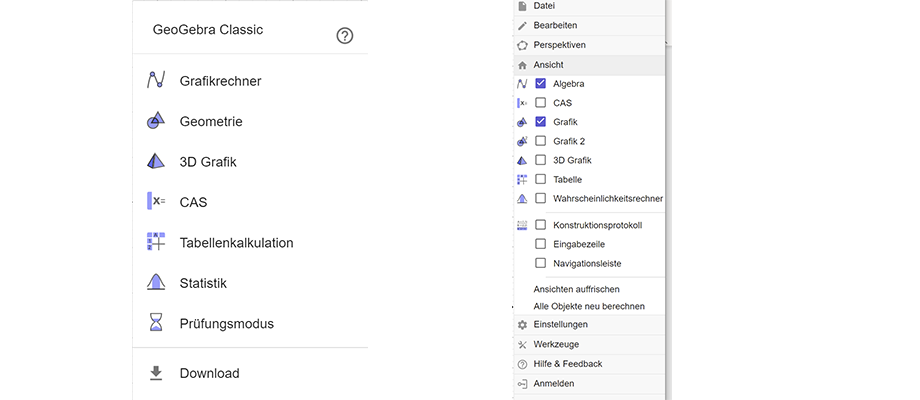
• In der Grafik-Ansicht kann man geometrische Objekte konstruieren. Parallel dazu erscheint die mathematische Beschreibung in der Algebra-Ansicht.
• In der Algebra-Ansicht kann man mathematische Objekte definieren. Parallel dazu erscheint die geometrische Konstruktion in der Grafik-Ansicht.
• In der CAS-Ansicht kann man Terme umformen, Gleichungen lösen sowie integrieren und differenzieren.
• In der Tabellen-Ansicht kann man Punktpaare zu Listen zusammenfassen um anschließend mit Hilfe der Regression die zugrundeliegende Funktionsgleichung zu ermitteln.
• Mit dem Wahrscheinlichkeitsrechner kann man Wahrscheinlichkeits- bzw. Dichtefunktionen und Verteilfunktionen berechnen.

Die Werkzeugleisten

Die Werkzeugleiste von GeoGebra verläuft horizontal am oberen Rand des Fensters. Sie ist zweigeteilt.

Bild

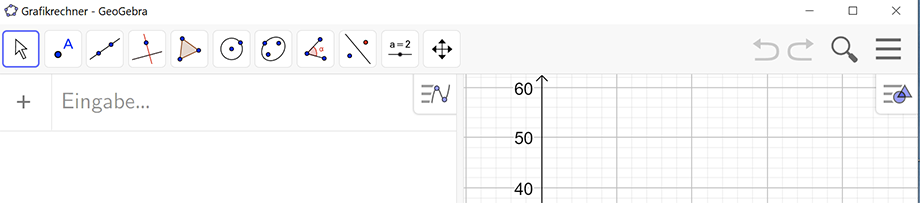
Im linken Bereich werden Icons angezeigt, welche Werkzeuge repräsentieren, die abhängig von der jeweiligen Ansicht sind. Klickt man auf eines der Werkzeuge, so werden unterhalb weitere, ähnliche Werkzeuge angezeigt.

Bild

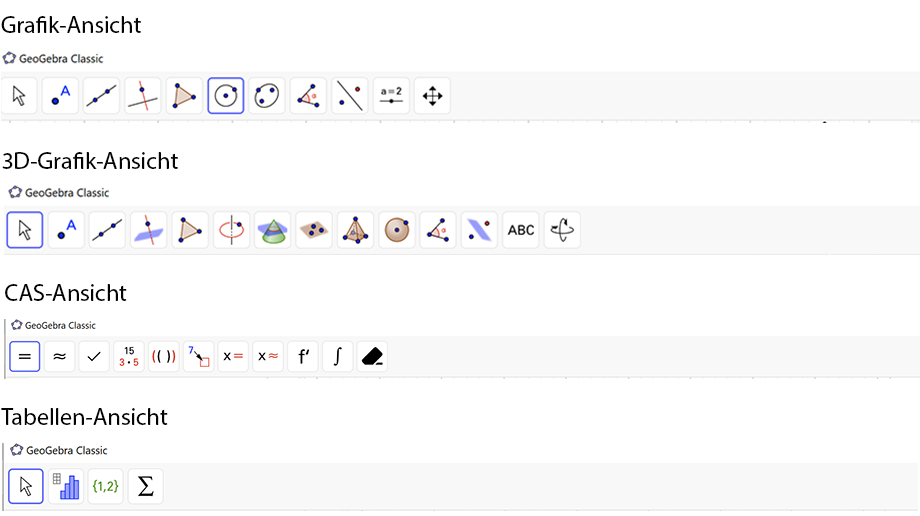
Im rechten Bereich werden die Werkzeuge für „Rückgängig“, „Wiederherstellen“ und „Lupe“ angezeigt. Klickst du auf „Lupe“, kommst du automatisch auf die Online-Plattform mit zahlreichen kostenlosen Unterrichtsmaterialien. Zudem kann ganz rechts die Menüleiste ein- bzw. ausgeblendet werden.

Die Gestaltungsleisten

Jede Ansicht (Grafik, Algebra, 3D-Grafik, CAS und Tabelle) verfügt über eine eigne Gestaltungsleiste, mit der verschiedene Grundeinstellungen für

1. die Ansicht selbst
2. die in der Ansicht enthaltenen Objekte

verändert werden können.

Bild

Ein- und ausblenden kann man die Gestaltungsleiste rechts oben im Fenster der jeweiligen Ansicht.

Gestaltungsleiste der Grafik-Ansicht

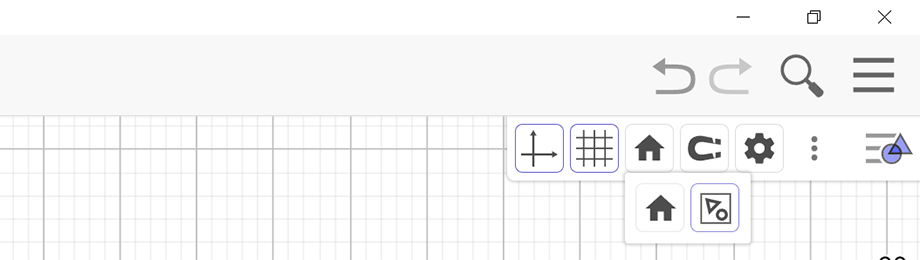
Klickt man in der Grafik-Ansicht auf das Icon der Gestaltungsleiste so lassen sich folgende Einstellungen vornehmen:

• Achsen anzeigen oder verbergen
• Koordinatengitter anzeigen oder verbergen
• Standardeinstellungen der Koordinatenachsen wieder herstellen
• Punkte an den Ecken der Koordinatengitter fangen
• Einstellungen öffnen
• Weitere Ansichten einblenden

Klickt man hingegen auf ein bestimmtes Icon der Werkzeugleiste, dann kann man die Eigenschaften (Farbe, Strichstärke, Linienart, Beschriftung,...) eines konkreten Objekts (Punkt, Gerade, Vektor, Kreis,...) verändern.

Sehr nützlich: Wenn man in der Grafik-Ansicht einmal den Überblick verloren hat, wo am Zeichenblatt sich überhaupt Inhalte befinden, kann man in der Gestaltungsleiste mittels dem Haus-Icon und dem Werkzeug mit dem "Dehnen-Pfeil" alle Inhalte sichtbar machen. 

Bild

Gestaltungsleiste der Algebra-Ansicht

Klickt man in der Algebra-Ansicht auf das Icon der Gestaltungsleiste so lassen sich folgende Einstellungen vornehmen:

• Sortierung der Zeilen in der Algebra Ansicht wählen. 
  • Sortieren nach freien und abhängigen Objekten
  • Sortieren nach dem Typ des Objekts (Punkte, Vektoren,...)
  • Sortieren der Objekte nach Ebenen, in denen sie konstruiert wurden
  • Sortieren nach der Reihenfolge der Konstruktion
  • Einstellungen öffnen
  • Weitere Ansichten einblenden

Bild

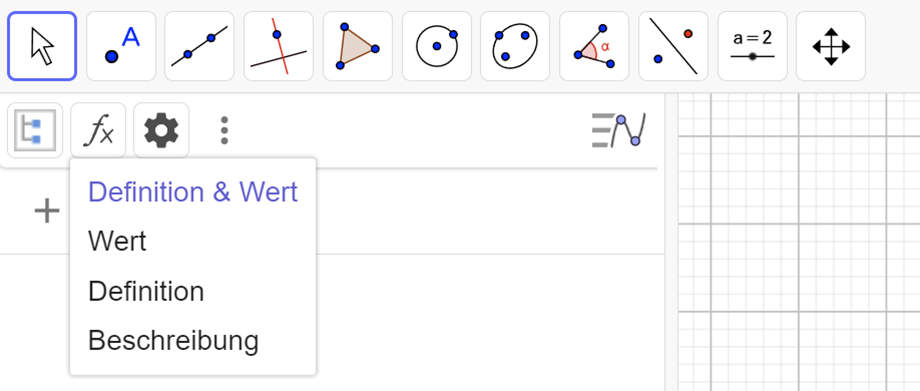
Gestaltungsleiste der CAS-Ansicht

Klickt man in der CAS-Ansicht auf das Icon der Gestaltungsleiste so lassen sich folgende Einstellungen vornehmen:

• Textformatierungen der Formelinhalte je Zeile, z.B.: Farbe, Fettschrift, Schrägschrift
• Einstellungen öffnen
• Weitere Ansichten einblenden

Bild

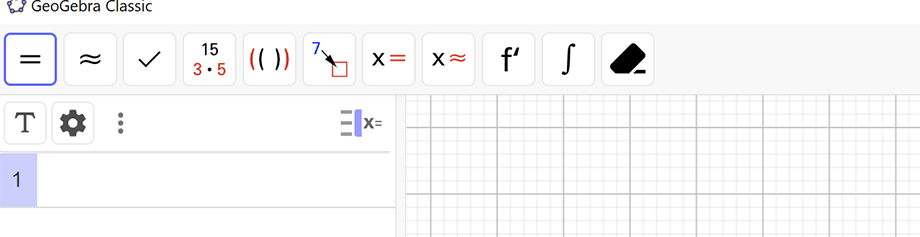
Gestaltungsleiste der Tabellen-Ansicht

• Textformatierungen der Formelinhalte je Zeile, z.B.: Fettschrift, Schrägschrift, Text-Bündigkeit

• Hintergrundfarbe

• Einstellungen öffnen
• Weitere Ansichten einblenden

Bild

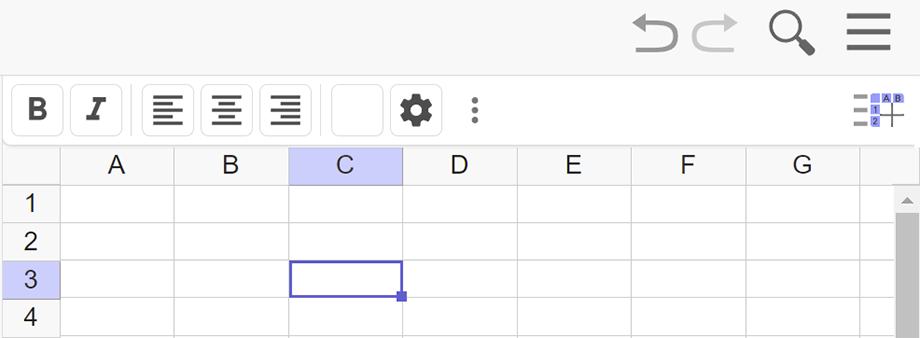
Gestaltungsleiste der 3D-Grafik-Ansicht

Klickt man in der 3D-Grafik-Ansicht auf das Icon der Gestaltungsleiste so lassen sich folgende Einstellungen vornehmen:

• Achsen anzeigen oder verbergen
• Koordinatengitter anzeigen oder verbergen
• Standardeinstellungen der Koordinatenachsen wieder herstellen
• Punkte an den Ecken der Koordinatengitter fangen
• Drehung der Ansicht starten bzw. stoppen
• Blickrichtung auf die 3D-Darstellung wählen: Grundriss, Aufriss bzw. Kreuzriss
• Art der Projektion wählen: Parallelprojektion, Perspektive mit Fluchtpunkt, 3D für rot-grün-3D-Brille, Schrägprojektion
• Einstellungen öffnen
• Weitere Ansichten einblenden

Bild

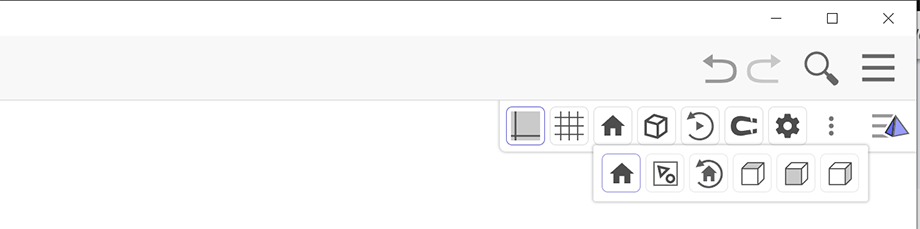
Die Menüleiste

Die GeoGebra Menüleiste wird mit dem Icon aus 3 Strichen, ganz rechts in der oben horizontal verlaufenden Werkzeugleiste, ein- und ausgeblendet. Sie enthält Menüs mit denen man Dateien öffnen oder abspeichern kann, mit der man die Hauptansichten wählen kann, oder mit denen man globale die Einstellungen ändern kann. 

Bild

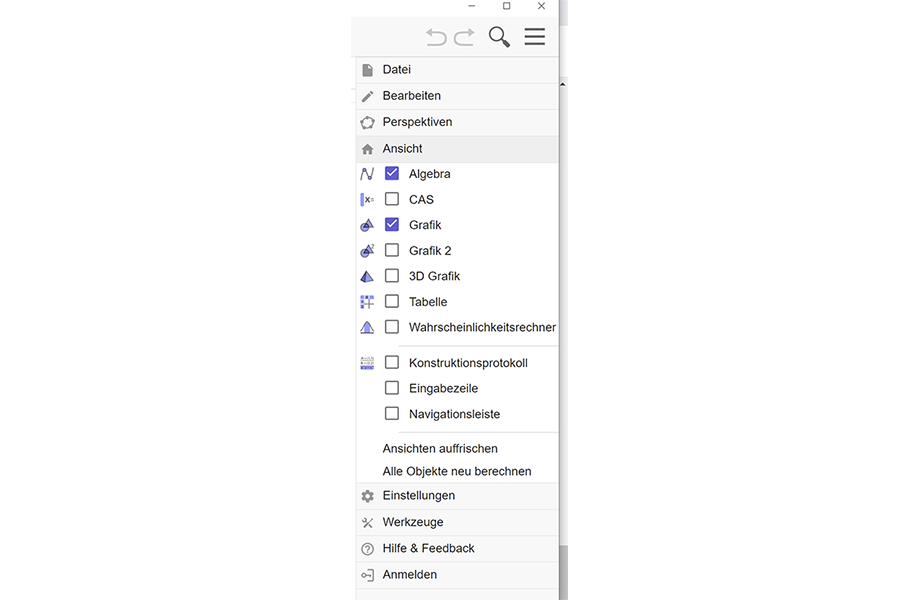
Die Eingabezeilen

Mit Hilfe der Eingabezeile und Befehlen kann man die algebraische Repräsentation eines mathematischen Objekts eingeben bzw. ändern. Die GeoGebra Eingabezeile kann über die Menüleiste und das Ansicht-Menü ein- bzw. ausgeblendet werden. Sie befindet sich dann am untersten Rand vom Fenster.

Bild

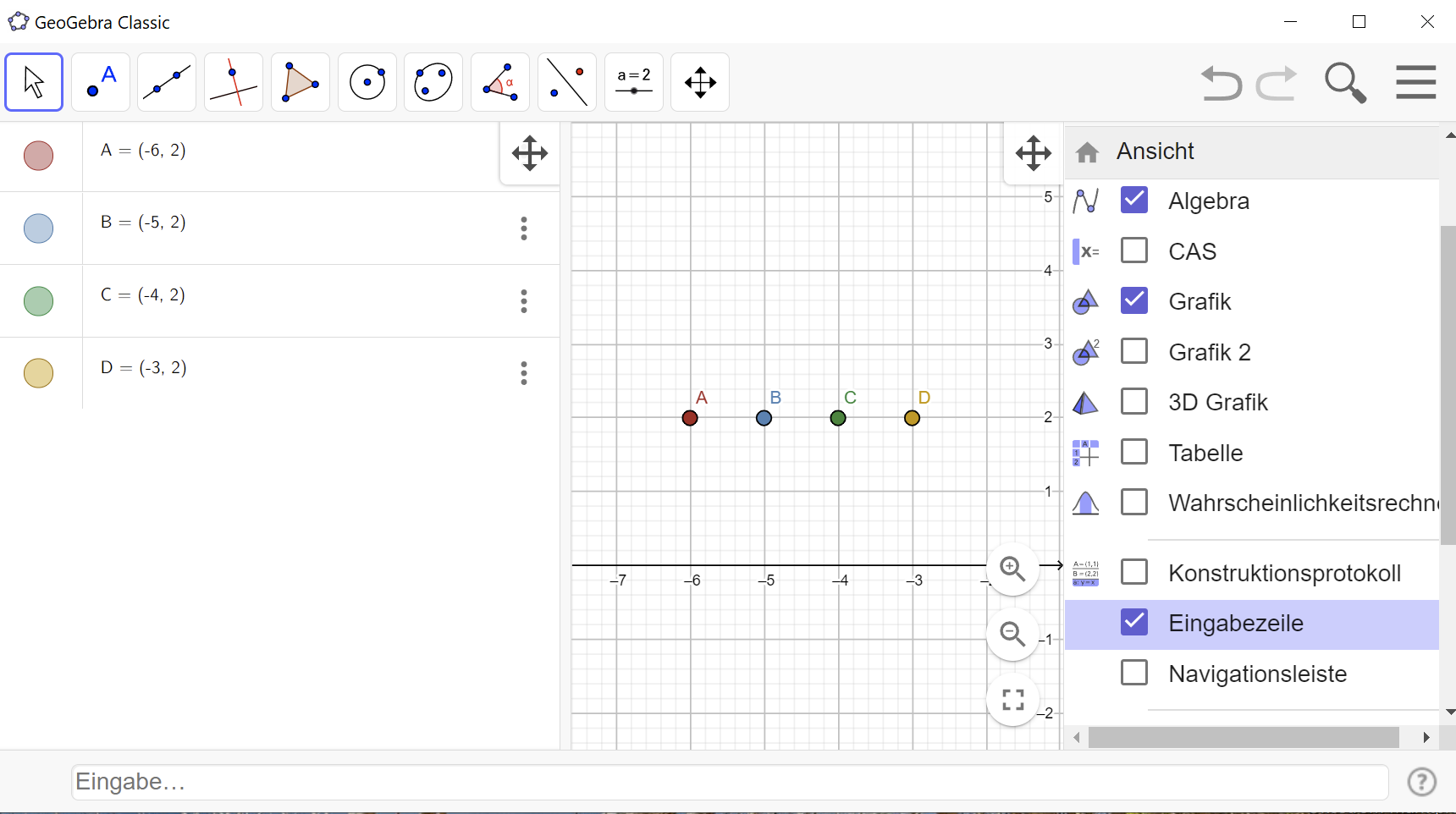
Ist die Algebra-Ansicht aktiviert, dann wird dort eine Algebra-Eingabezeile angezeigt, wenn die oben beschriebene GeoGebra Eingabezeile ausgeblendet ist.

Bild

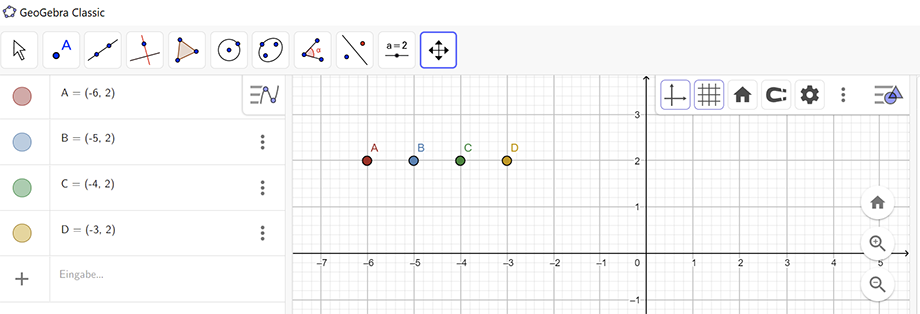
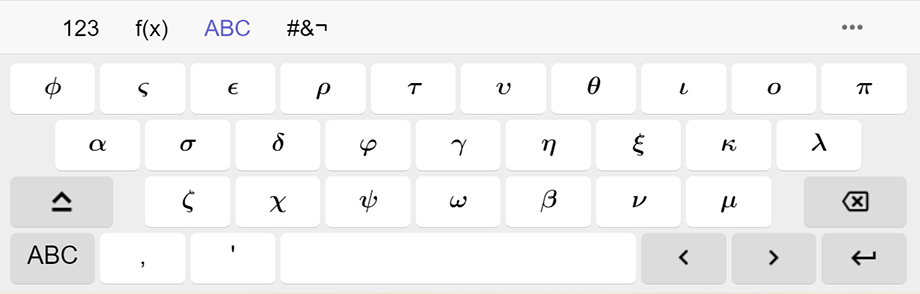
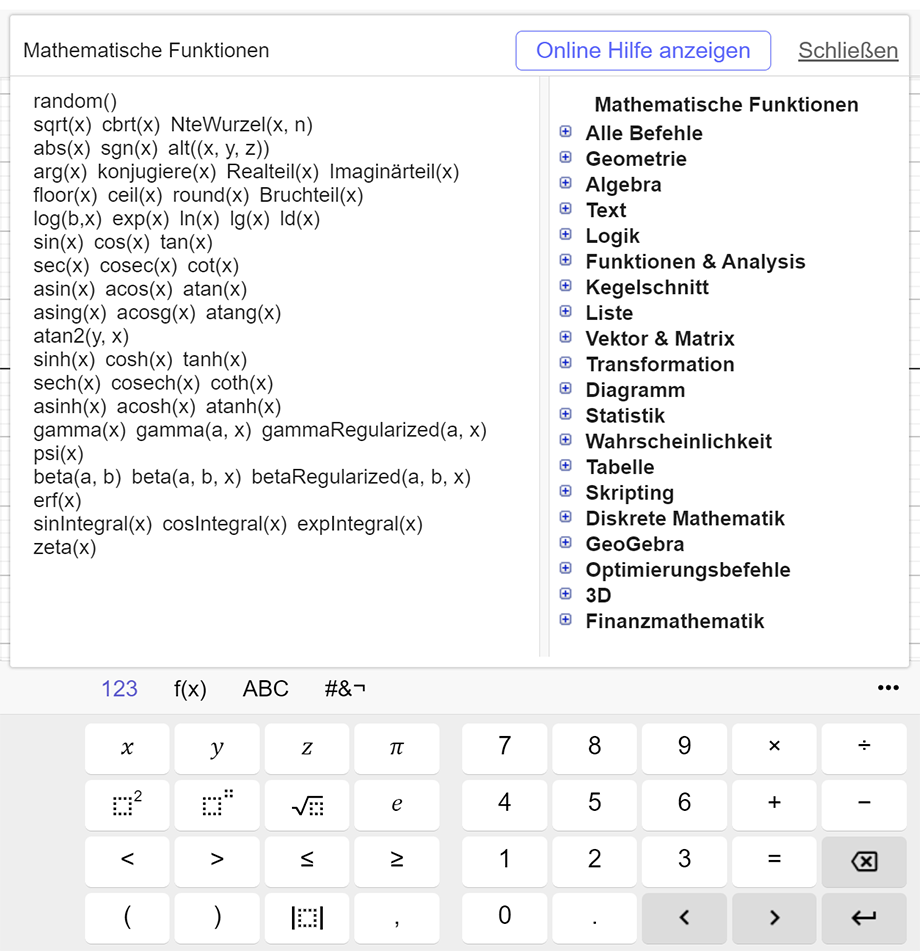
Die virtuelle Tastatur

Wenn man GeoGebra erstmalig startet, dann erscheint links die Algebra-Ansicht und rechts die Grafik-Ansicht. Darunter wird eine virtuelle Tastatur angezeigt, die mit der Maus bedient wird. 

Bild

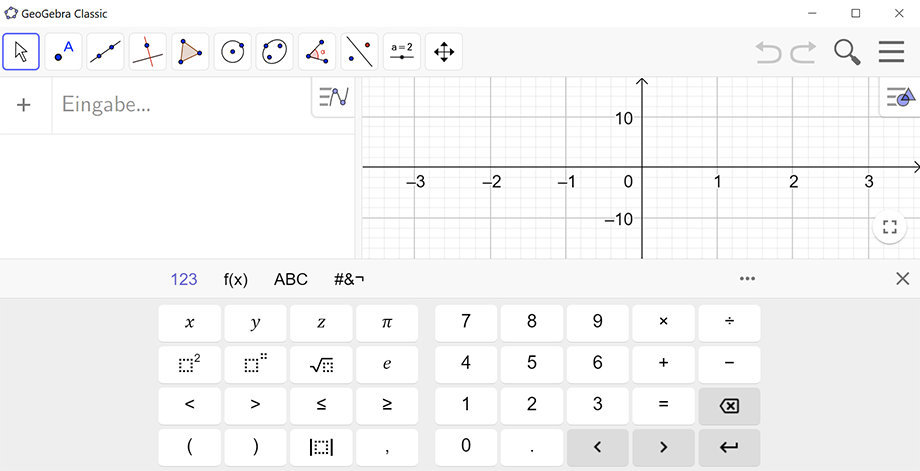
Sollte die virtuelle Tastatur mal unsichtbar werden, dann klickt man auf das "+" in der Algebra-Eingabezeile und wählt "Ausdruck". Dann wird die virtuelle Tastatur eingeblendet.

Bild

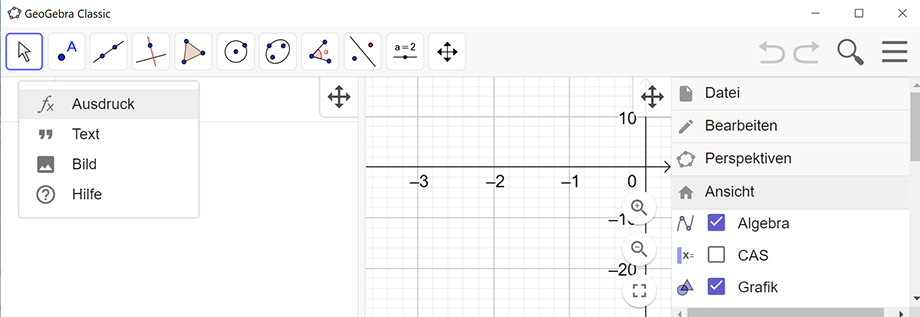
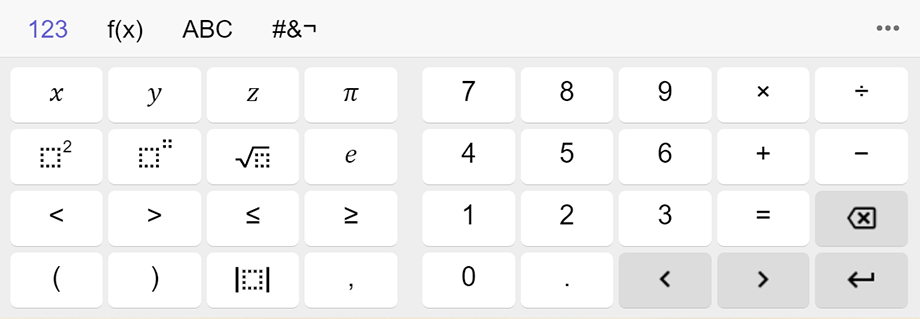
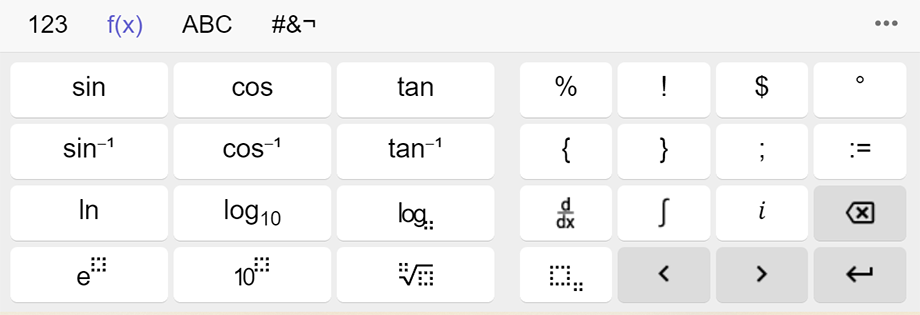
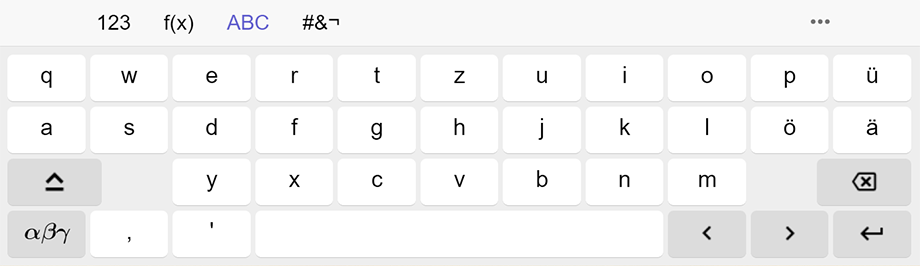
Bei der virtuelle Tastatur kann zwischen unterschiedlichen Tastatur-Layouts umgeschaltet werden.

Bild

Bild

Bild

Bild

Bild

Bild

Bild

Lektion 2: Dateihandling und Dateneingabe in GeoGebra

In dieser Mikro-Lerneinheit verschaffen wir uns einen Überblick über den "Datei" - Eintrag in der Menüliste und über diverse programmspezifische Anforderungen an die Eingabe.

Zuerst verschaffst du dir zuerst einen Überblick darüber, wie du eine neue oder bestehende GeoGebra Datei mit der Datei-Endung .ggb öffnest, bearbeitest und wieder abspeicherst. Weiters ist es unbedingt erforderlich zu wissen, wie man die diversen Eingaben korrekt eintippen muss, damit sie von GeoGebra korrekt verarbeitet werden können.

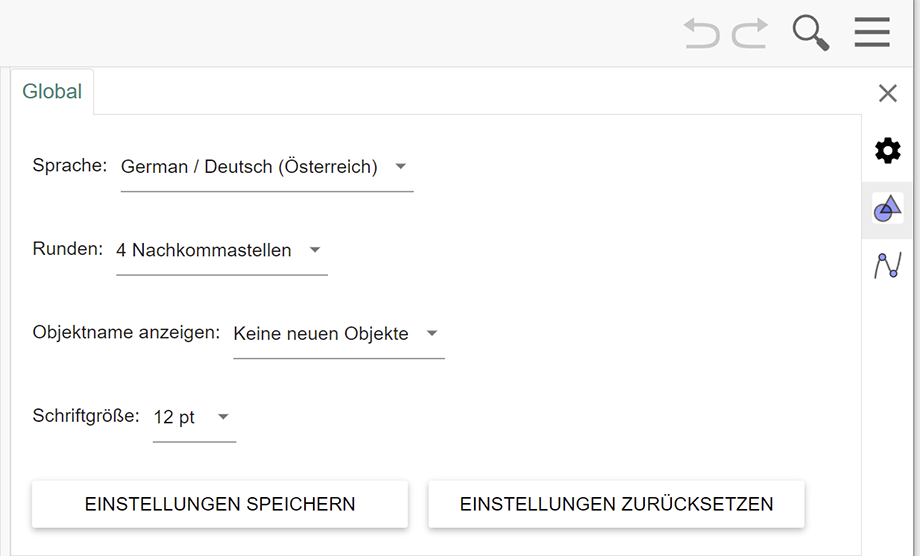
"Einstellungen" - Eintrag in der Menüleiste

Als Erstes sollte man einige globale Einstellungen vornehmen. Die Sprache, die Anzahl der Nachkommastellen, ob Objekte in der Grafik-Ansicht sichtbar benannt werden und die Schriftgröße (12pt) wählt man in der Menüleiste unter "Einstellungen". 

Bild

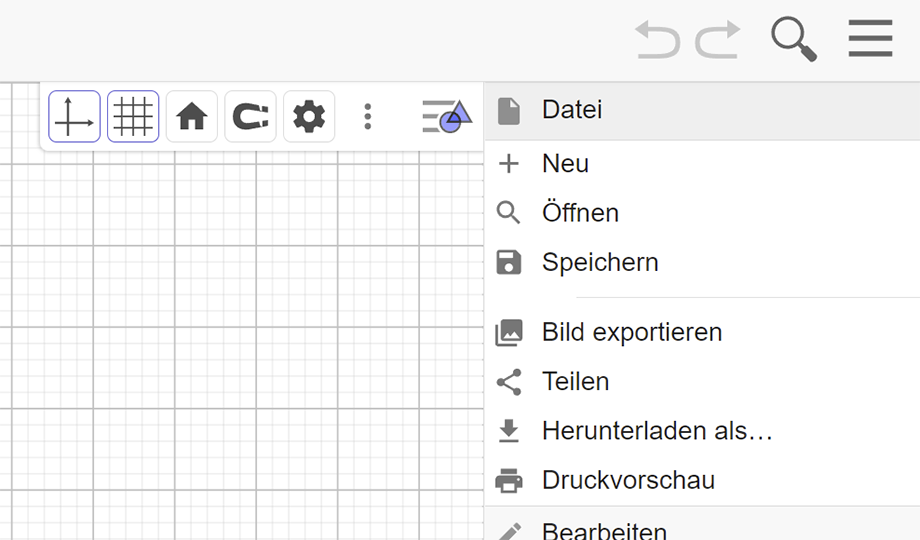
„Datei“ – Eintrag in der Menüleiste

Beschäftigen wir uns zunächst damit, wie wir ein GeoGebra-Arbeitsblatt öffnen und speichern können.

• „Neu“ erstelle ein neues leeres Arbeitsblatt

• „Öffnen“ macht dasselbe wie ein Klick auf die „Lupe“ in der Werkzeugleiste:

  • „online“: In der Hauptansicht vom GeoGebra Fenster wird die GeoGebra-Online-Plattform mit zahlreichen kostenlosen Unterrichtsmaterialen angezeigt und man kann eine Datei auswählen, öffnen, bearbeiten und abspeichern.

  • „lokal“: Über den Button ganz links oben im Fenster kann man auf lokal am Computer gespeicherte Dateien zugreifen

• „Speichern“ ermöglicht das Abspeichern vom gesamten Arbeitsblatt in einer GeoGebra-Datei vom Typ .ggb.

• „Bild exportieren“ ermöglicht es die Grafik-Ansicht als pixelbasierte Bilddatei vom Typ .png abzuspeichern.

• „Teilen“ ermöglicht es, zuvor auf der GeoGebra-Online-Plattform abgespeicherte Arbeitsblätter, über soziale Netzwerke oder als direkter Link weiterzugeben.

• „Herunterladen als…“ ermöglicht das Abspeichern des aktuell sichtbaren Ausschnitts der Grafik-Ansicht, in verschiedenen Dateiformaten wie .png, .svg oder .pdf.
  Will man mehr Einfluss – z.B. einen transparenten Bildhintergrund - auf die Parameter der Bilddatei haben, dann empfiehlt sich der Befehl „ExportImage“.
  z.B.: ExportImage("filename", "beispiel_4410_1.svg", "type", "svg", "transparent", "true")

• „Druckvorschau“ ermöglicht das Ausdrucken des aktuell sichtbaren Ausschnitts der Grafik-Ansicht

Bild

Anforderungen an die Eingabe:

Mit Hilfe der Eingabezeile und Befehlen kann man die algebraische Repräsentation eines mathematischen Objekts eingeben bzw. ändern. Dabei sind folgende Regeln zu beachten:

• Dezimalzahlen erfordern die englische Schreibweise, d.h. das Komma wird als Punkt geschrieben. Beispiel: ½ als 0.5 nicht als 0,5
• Hochzahl einer Potenz erzeugt man mit der „Dach-Taste“, also etwa 2^x durch 2^x
• Fakultät wird als n! geschrieben und ist das Produkt aller natürlichen Zahlen größer Null und kleiner gleich n
• Binomialkoeffizient n über k wird als nCr(n,k) geschrieben und besagt, wie viele Möglichkeiten es gibt, k Elemente aus einer Menge von n Elementen auszuwählen
• Permutation ohne Zurücklegen nPr(n,k) besagt, wie viele Möglichkeiten es ohne Zurücklegen gibt, k Elemente aus einer Menge von n unterscheidbaren Elementen auszuwählen
• Komplexe Zahl im CAS: Die Eingabe muss in der Form (a+bi) erfolgen, nicht aber als (a+ib).
• Punkte werden mit Großbuchstaben eingegeben: A=(2,2)
• Vektoren werden mit Kleinbuchstaben eingegeben v=(1,1,2)
• Listen werden mit dem Kleinbuchstaben l und einer Zahl innerhalb einer geschwungenen Klammer eingegeben: l1={1,2,3} oder l2={4,5,6}. Am einfachsten erzeugt man Listen in der Listenansicht.
• Matrizen werden mit dem Kleinbuchstaben m und einer Zahl innerhalb einer geschwungenen Klammer als Liste von Listen eingegeben: m1= {{1, 2, 3}, {4, 5, 6}} oder m1={l1,l2}

• Eulersche Zahl \(e\) darf nicht als Buchstabe „e“ eingegeben werden, sondern wird
  • entweder als Sonderzeichen über die virtuelle Tastatur (im Bereich 123 zu finden) eingegeben
  • oder mittels „Alt + e“ über die Tastatur
• Kreiszahl Pi wird
  • durch das Wort pi oder Pi eingegeben
  • oder als Sonderzeichen über die virtuelle Tastatur (im Bereich 123 zu finden) eingegeben
  • oder mittels „Alt P“ über die Tastatur
• Imaginäre Einheit i darf nicht als Buchstabe „i“ eingegeben werden, sondern wird
  • entweder als Sonderzeichen über die virtuelle Tastatur (im Bereich f(x) zu finden) eingegeben
  • oder mittels „Alt + i“ über die Tastatur
• Unendlich-Zeichen \(\infty \) wird 
  • entweder als Sonderzeichen über die virtuelle Tastatur eingegeben
  • durch das Wort infinity oder Infinity eingegeben
  • oder mittels „STRG + U“ über die Tastatur.

• Zuweisung := vs Gleichung = In der CAS-Ansicht werden Variable und Terme mit einem den Gleichheitszeichen vorgesetzten Doppelpunkt „:=“ zugewiesen, nicht so in der Algebra-Ansicht
  • CAS-Eingabe: f(x):=2x^2
  • Algebra-Eingabe: f(x)=2x^2
• Mal-Rechenzeichen „*“ der Multiplikation muss in der CAS-Ansicht verpflichtend in der Form „*“ eingegeben werden, nicht so in der Algebra-Ansicht
  • CAS-Eingabe: a*(b+c)
  • Algebra-Eingabe: a(b+c)
• Brüche werden in Form einer Division angeschrieben, wobei sowohl Zähler als auch Nenner in runde Klammern gesetzt werden sollten.
• Variablen existieren nur ein Mal innerhalb eines Arbeitsblattes. Es kann der Variablen in einer nachfolgenden CAS-Eingabe kein neuer Wert zugewiesen werden. Variablen, die in der Algebra-Ansicht definiert wurden, werden in der CAS-Ansicht nicht erneut dargestellt, können aber verwendet werden.

• Funktionen kann man durch den Funktionsterm einzugeben, man kann aber auch y= oder f(x)= voran setzen.
• Betragsfunktion gibt man als abs(..) ein, wobei die Zahl zwischen runden Klammern gesetzt wird.
• Signumfunktion liefert Vorzeichen, die man mit Hilfe der Signum-Funktion sign(x) ermittelt
  • Liefert +1 für positive Zahlen, -1 für negative Zahlen und 0 für null
• Rundungsfunktionen erhält man mit Hilfe
  • round(x), wodurch auf die nächste ganze Zahl gerundet wird
  • ceil(x), wodurch auf die nächste ganze Zahl aufgerundet wird
  • floor(x), wodurch auf die nächste ganze Zahl abgerundet wird
• Wurzel zieht man mit Hilfe von sqrt(x)
• Logarithmen berechnet man mit Hilfe von ln(x), log(x) bzw. mit log10(x) oder log2(x)
• Winkelfunktionen berechnet man mit sin(x), cos(x), tan(x),…
• Umkehrung der Winkelfunktionen liefern mit
  • arcsind(x) das Ergebnis in Grad
  • arcsin(x) das Ergebnis in Radianten

Unterschied freie und abhängige Objekte

• Freie Objekte (z.B.: 2 Punkte A, B) hängen nicht von der Position oder vom Wert bereits zuvor erstellter Objekte ab. Werden freie Objekte über ihre "Einstellungen" fixiert, können sie nicht mehr gezogen und damit auch nicht mehr in ihrer Position am Zeichenblatt verändert werden.
• Abhängige Objekte (z.B.: die Strecke AB)  hängen von der Position oder vom Wert bereits zuvor erstellter freier Objekte ab. Löscht man das zugrunde liegende freie Objekt, so löscht man auch das abhängige Objekt.

Statische und dynamische Texte

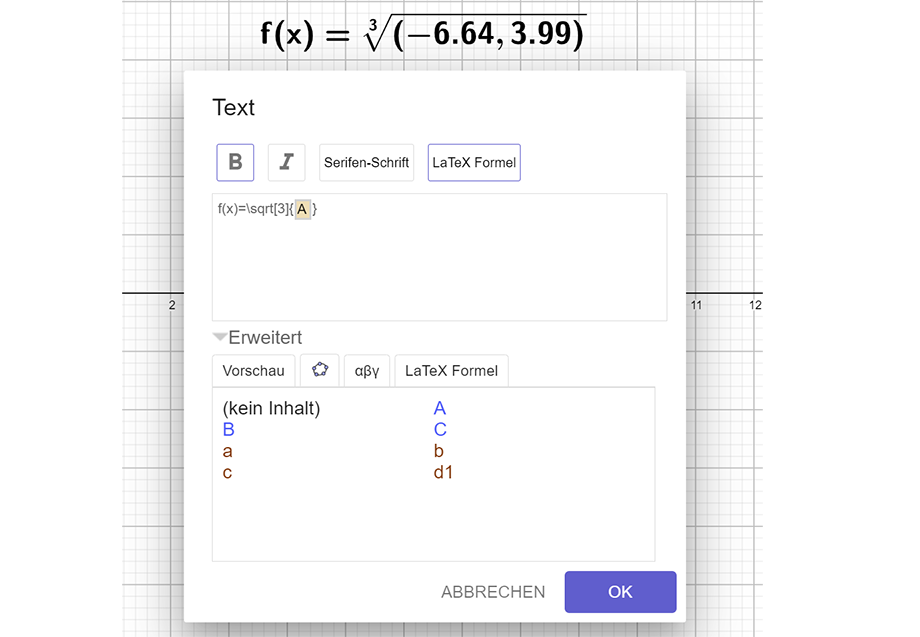
Die Eingabemaske für Texte wird über die Werkzeugleiste und das Icon "ABC Text" eingegeben. Über "Erweitert" kann man 4 Kartei-Reiter (Vorschau, GeoGebra-Symbol, Griechischen Zeichensatz und vordefinierte LaTeX Formeln) anzeigen.

• Statischer Text wird über die Tastatur eingegeben und ist von Objekten und Änderungen an Objekten unabhängig. Statischer Text kann in Form von ASCII Code oder als LaTeX-Code eingegeben werden. Während mit ASCII Code die von der Tastatur vertrauten Buchstaben und Ziffern und einige darüber hinausgehende Sonderzeichen eingegeben werden können, kann man mit LaTeX-Code ganze Formeln (samt Wurzel- und Integralzeichen oder Brüchen) eingeben.
• Dynamischer Text wird mit Hilfe der im Kartei-Reiter mit dem GeoGebra-Symbol enthaltenen Objekten erstellt. 
• Statischer und Dynamischer Text zusammen ermöglichen Texte mit Koordinaten zu vereinen.

Bild

Geogebra Binomial (Befehl)

• Binomial( <Anzahl der Versuche>, <Erfolgswahrscheinlichkeit> )
• Mit dem Befehl Binomial (n, p) erzeugt man in der Grafik-Ansicht ein Balkendiagramm.
  • Der Parameter n steht dabei für die Anzahl der von einander unabhängigen Bernoulli-Versuche.
  • Der Parameter p steht für die Erfolgswahrscheinlichkeit pro Versucht

Beispiel

• Gegeben:
  • n=20
  • p=0,9
• Gesucht:
  • Balkendiagramm der Binomialverteilung
• Ausführung:
  • Syntax: Binomial( <Anzahl der Versuche>, <Erfolgswahrscheinlichkeit> )
  • Geogebra Grafik-Ansicht: Binomial(20, 0.9)
  • Anmerkung: x-Achse auf 0 .. 22 skalieren; y-Achse auf 0 .. 0,5 skalieren
• ​Lösung:
  • Wir erhalten ein Balkendiagramm der Binomialverteilung.
  • Der höchste Balken entspricht dem zugehörigen Erwartungswert \(E(x) = \mu \)

Beispiel

• Gegeben:
  • n=20
  • p=0,9
• Gesucht:
  • Erwartungswert \(E(x) = \mu \) der Binomialverteilung
  • Standardabweichung \(\sigma\) der Binomialverteilung
• Ausführung:
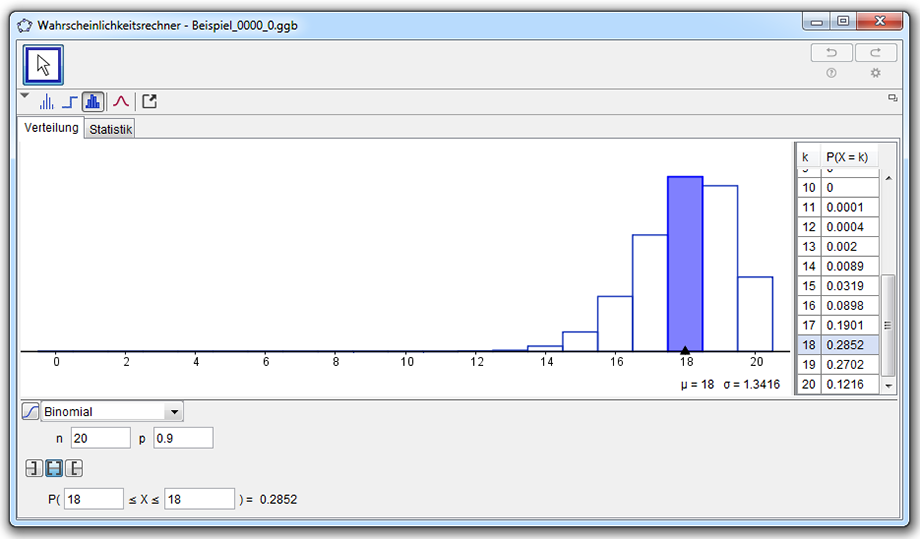
  • Geogebra → Ansicht → Wahrscheinlichkeitsrechner
  • Im Feld für die Verteilung von Normal auf → Binomial umstellen
  • n=20 und p=0.9 eingeben
  • Die Klammerausdrücke können unbeachtet bleiben
• ​Lösung:
  • Wir erhalten ein Balkendiagramm der Binomialverteilung.
  • Wir erhalten den zugehörigen Erwartungswert zu \(E(x) = \mu = 18\)
  • Wir erhalten die zugehörige Streuung zu \(\sigma = 1,3416\)

Bild

Geogebra InversNormal (Befehl)

• InversNormal[ <Mittelwert>, <Standardabweichung>, <Wahrscheinlichkeit> ]
• Mit dem Befehl InversNormal (μ, σ , P] berechnet man jene Zufallsvariable X, welche die gegebene Wahrscheinlichket P als Fläche unter der Gauß'schen Glockenkurve besitzt.

Beispiel

• Gegeben:
  • Erwartungswert μ = 1005 mm
  • Standardabweichung σ = 5 mm
  • Fläche = 0,025 bzw. Wahrscheinlichkeit P = 2,5%
• Gesucht:
  • Zufallsvarialble X
• Ausführung:
  • Syntax: InversNormal[ <Mittelwert>, <Standardabweichung>, <Wahrscheinlichkeit> ]
  • Geogebra - CAS Ansicht: InversNormal[1005, 5, 0.025] → X=x₁ = 995,25
• Lösung
  • Für die Zufallsvariable X=x₁ = 999,25 mm beträgt bei einer μ = 1005 mm und σ = 5 mm verteilten Normalverteilung die Wahrscheinlichkeit 2,5% bzw. die Fläche unter der Gauß'schen Glockenkurve 0,025

Beispiel

• Gegeben:
  • Erwartungswert μ = 1005 mm
  • Standardabweichung σ = 5 mm
  • Fläche = 0,95 bzw. Wahrscheinlichkeit P = 95%
• Gesucht:
  • Ermitteln Sie dasjenige um μ symmetrische Intervall, in dem 95 % der Zufallswerte liegen.
• Ausfühung:
  • untere Grenze: Fläche links von der unteren Grenze: \(\dfrac{{1 - 0,95}}{2} = 0,025\)
    • Syntax: InversNormal[ <Mittelwert>, <Standardabweichung>, <Wahrscheinlichkeit> ]
    • Geogebra - CAS Ansicht: InversNormal[1005, 5, 0.025] → x₁ = 995,25
  • obere Grenze: Fläche links von der oberen Grenze: \(\dfrac{{1 - 0,95}}{2} + 0,95 = 0,975\)
    • Syntax: InversNormal[ <Mittelwert>, <Standardabweichung>, <Wahrscheinlichkeit> ]
    • Geogebra - CAS Ansicht: InversNormal[1005, 5, 0.975] → x₂ = 1014,75
• Lösung:
  • Das symmetrische Intervall, in dem mit einer Wahrscheinlichkeit P=95% alle Zuvallsvariablen X einer μ = 1005 mm und σ = 5 mm verteilten Normalverteilung liegen, lautet: [995,2; 1 014,8]
• Grafische Darstellung

  • Der Befehl mit der Syntax: Normal[μ, σ, x, false] erzeugt eine Darstellung der Wahrscheinlichkeitsdichtefunktion der Normalverteilung f

    • Geogebra Grafik-Ansicht: Normal(1005, 5, x, false)

  • ​Der Befehlt mit der Syntax: Integral(<Funktion>, <untere Grenze>, <obere Grenze>) berechnet das bestimmte Integral der Funktion f zwischen unterer und oberer Grenze und schattiert die Fläche über die integriert wurde.

    • Geogebra Grafik-Ansicht: Integral(f, 995.25, 1014.75)

Geogebra Normal (Befehl)

• Normal[ <Erwartungswert>, <Standardabweichung>, <Wert der Variablen x₁> ]
• \(P\left( {X \le x_1} \right)\) einer \({\rm{N}}\left( {\mu ,\sigma } \right)\) Normalverteilten Zufallsvariablen X berechnen
• Mit dem Befehl Normal[μ, σ , x₁] berechnet man die Wahrscheinlichkeit P dafür, dass eine Zufallsvariable X kleiner oder gleich einem Grenzwert x₁ ist. Das Resultat entspricht der Fläche unter der Gauß'schen Glockenkurve, welche links von x₁ liegt.

Beispiel

• Gegeben:
  • ​Erwartungswert μ = 12,000 mm
  • Standardabweichung σ = 0,06 mm
  • untere Grenze x₁ = 11,96 mm
  • obere Grenze x₂ = 12,04 mm
• Gesucht:
  • Wahrscheinlichkeit, dass eine Zufallsvariable X zwischen einer unteren x₁ und einer oberen x₂ Grenze liegt
  • ​\(P\left( {{x_1} \le X \le {x_2}} \right)\) einer \({\rm{N}}\left( {\mu ,\sigma } \right)\) -verteilten Zufallsvariablen X berechnen
• Ausführung:
  • Syntax: Normal[μ, σ , x₂] - Normal[μ, σ , x₁]
  • Geogebra Algebra-Ansicht: Normal[12, 0.06, 12.04] - Normal[12, 0.06, 11.96] → (0,7475 - 0,2525 =) 0,495
• Lösung
  • Die Wahrscheinlichkeit, daß ein μ = 12,000 mm und σ = 0,06 mm verteilter Zufallswert zwischen x₁ = 11,96 mm und x₂ = 12,04 mm liegt, beträgt 49,5%
• Grafische Darstellung
  • Der Befehl mit der Syntax: Normal[μ, σ, x, false] erzeugt eine Darstellung der Wahrscheinlichkeitsdichtefunktion der Normalverteilung f
    • Geogebra Grafik-Ansicht: Normal(12, 0.06, x, false)
  • ​Der Befehlt mit der Syntax: Integral(<Funktion>, <untere Grenze>, <obere Grenze>) berechnet das bestimmte Integral der Funktion f zwischen unterer und oberer Grenze und schattiert die Fläche über die integriert wurde.
    • Geogebra Grafik-Ansicht: Integral(f, 11.96, 12.04)

Satz von Thales

Interaktive Illustration auf GeoGebra.org anzeigen

Bewege den Punkt P entlang vom Halbkreis und beobachte wie sich die beiden Winkel immer zu 90° aufsummieren.

Exponentialfunktion

Interaktive Illustration auf GeoGebra.org anzeigen

• Regler a: Verändere die Basis
• Regler c: Verändere den Faktor

Natürliche Exponentialfunktion

Interaktive Illustration auf GeoGebra.org anzeigen

• Regler \(\lambda\): Entscheidet über Wachstum oder Zerfall
• Regler N₀: Entscheidet über Startwert