Elektrische Ladung
Hier findest du folgende Inhalte
Formeln
Vorab eine Mindmap zu den Inhalten dieser Mikro-Lerneinheit
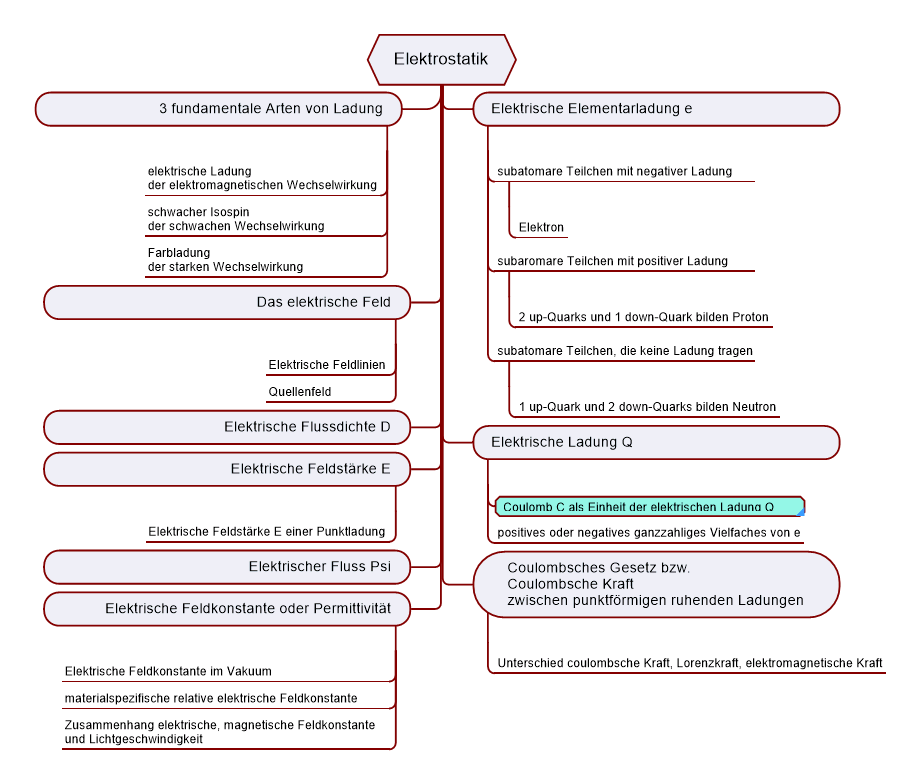
Elektrostatik
Die Elektrostatik ist der einfachste Fall der Elektrodynamik. Sie beschreibt die Felder, die von ruhenden elektrischen Ladungen ausgehen, sowie die Kräfte, die zwischen ruhenden elektrischen Ladungen wirken.
Drei fundamentale Arten von Ladung
Gemäß dem Standardmodell der Elementarteilchen ist Ladung eine fundamentale Eigenschaft von Teilchen. Zusammen mit der Masse des Teilchens, bestimmen die 3 Arten von Ladung, welcher der 4 Wechselwirkungen ein Teilchen unterliegt. Alle drei Arten von Ladungen treten quantisiert auf, d.h. sie können nur bestimmte, diskrete Werte annehmen. Die Ladung eines zusammengesetzten Teilchens, z.B. eines Atoms, setzt sich aus der Summe der Ladungen seiner Einzelteilchen (Elektronen, Quarks) zusammen. Die Summe der Ladung aller Teilchen eines Systems bleibt über alle ablaufenden Prozesse hinweg erhalten.
Es gibt 3 fundamentale Arten von Ladung, die bestimmen welcher Wechselwirkung ein Teilchen unterliegt:
- die elektrische Ladung der elektromagnetischen Wechselwirkung
- den schwachen Isospin der schwachen Wechselwirkung
- die Farbladung der starken Wechselwirkung
- zur vierten Wechselwirkung, der Gravitation, gibt es keine Ladung, die Masse hat aber eine vergleichbare Bedeutung, sie unterliegt aber (noch) nicht der Quantentheorie
- es gibt keine magnetische Ladung, somit keine magnetische Monopole
Elektrische Elementarladung e
Elektrische Elementarladung → Elektrostatik; Elementarmagnetismus → Magnetostatik;
Die Elementarladung ist eine fundamentale Eigenschaft von elektrisch geladenen Teilchen und Ausgangspunkt der Elektrostatik. "Fundamentale" Eigenschaft bedeutet, dass die elektrische Ladung durch keine andere physikalische Größe erklärbar ist. Die Elementarladung ist daher eine Naturkonstante, deren Wert exakt \(e = 1,602\,176\,634 \cdot {10^{ - 19}}C\) beträgt. Das Coulomb ist also die Einheit der elektrischen Elementarladung.
Folgende subatomaren Teilchen tragen negative elektrische Ladung:
- Elektronen: -1e
- Myonen: -1e
- Tauonen: -1e
- down-Quark: -1/3 e
- strange Quark: -1/3 e
- bottom-Quark: -1/3 e
Folgende subatomaren Teilchen tragen positive elektrische Ladung:
- up-Quark: +2/3 e
- charm Quark: +2/3 e
- top-Quark: +2/3 e
Nicht alle subatomaren Teilchen tragen Ladung.
- Elektron-Neutrino, Myon-Neutrino, Tau-Neutrino, Photonen, ... sind keine Träger elektrischer Elementarladung
Die elektrische Ladung des Protons ist exakt gleich groß wie die elektrische Ladung des Elektrons. Die Ladung des Protons ist positiv, die Ladung des Elektrons ist negativ. Die beiden Ladungen sind einander entgegengesetzt. Das Neutron ist elektrisch neutral, also nicht geladen.
Während das Elektron fundamental, also unteilbar ist, setzt sich das Proton und das Neutron seinerseits aus 3 ihrerseits fundamentalen Quarks zusammen, welche die eigentlichen Träger der elektrischen Ladung im Proton bzw. Neutron sind. Quarks können aber auf Grund eines quantenmechanischen Effekts, der „Confinement“ genannt wird, nicht allein sondern nur als Zusammensetzung aus 2, 3 oder 5 Quarks existieren. Lediglich Protonen und im Atomkern gebundene Neutronen sind stabil.
- Das Elektron ist fundamental, also aus keinen weiteren subatomaren Teilchen aufgebaut. Es ist mit -e negativ geladen.
- Ein Proton besteht aus zwei up-Quarks (+2/3) und einem down-Quark (-1/3). Es ist positiv geladen. Für die elektrische Ladung des Protons ergibt sich:
\(\left( {2 \cdot \dfrac{2}{3} - \dfrac{1}{3}} \right) \cdot e = \dfrac{{4 - 1}}{3} \cdot e = e\)
- Ein Neutron besteht aus einem up-Quark (+2/3) und zwei down-Quarks (-1/3) . Es ist elektrisch neutral. Für die elektrische Ladung des Neutrons ergibt sich:
\(\left( {\dfrac{2}{3} - 2 \cdot \dfrac{1}{3}} \right) \cdot e = \dfrac{{2 - 2}}{3} \cdot e = 0\)
Elektrische Ladung Q
Elektrische Ladung → Elektrostatik; Polstärke → Magnetostatik;
Die elektrische Ladung Q ist immer ein ganzzahliges, positives oder negatives Vielfaches der Elementarladung e. Die elektrische Ladung Q ist also die Summe der Elementarladungen e. Das Coulomb ist also die Einheit der elektrischen Ladung.
\(\eqalign{ & Q = n \cdot e{\text{ mit n}} \in {\Bbb Z}{\text{ (Menge der ganzen Zahlen)}} \cr & {\text{Q = }}{{\text{Q}}_ + } + {Q_ - } \cr} \)
Wobei Q+ für Protonen und Q- für Elektronen steht.
Alle Ladungen Q sind von einem elektrischen Feld \(\overrightarrow E \) umgeben. Die elektrische Ladung verändert nämlich den umgebenden Raum, indem sie dort ein elektrisches Feld erzeugt.
Coulomb C
Coulomb → Elektrostatik; Weber → Magnetostatik;
Das Coulomb C ist die Einheit der elektrischen Ladung. 1 Coulomb ist jene elektrische Ladung, die innerhalb von einer Sekunde durch den Querschnitt eines Leiters transportiert wird, in dem ein Strom von 1 Ampere fließt.
Die Einheit der Ladung Q ergibt sich gemäß folgender Einheitengleichung
\(\left[ Q \right] = \left[ I \right] \cdot \left[ t \right] = A \cdot s = C = \dfrac{{Nm}}{V}\)
Wenn elektrischer Strom fließt, bewegen sich elektrische Ladungsträger
\(\eqalign{ & 1{\text{C}} = 1{\text{A}} \cdot 1{\text{s}} \cr & {\text{Q = n}} \cdot {\text{e}} \cr & {\text{n = }}\dfrac{Q}{e} = \dfrac{{1\operatorname{C} }}{{1,602{\mkern 1mu} 176{\mkern 1mu} 634 \cdot {{10}^{ - 19}}C}} \approx 6,2415 \cdot {10^{18}} \cr} \)
Damit ein Strom von 1A für die Dauer von 1 Sekunde fließt, müssen sich in dieser Zeitspanne 6,2 Trillionen Elektronen durch den Leiterquerschnitt bewegen.
Bei Gleichstrom bewegen sich die Elektronen physikalisch vom Minus- zum Pluspol, bei Wechselstrom schwingen die Elektronen im Leiter abhängig von der Frequenz hin und her, ohne sich makroskopisch über die Amplitude der Schwingung hinaus zu bewegen.
Coulombsche Kraft zwischen zwei punktförmigen ruhenden Ladungen
Coulombsches Gesetz → Elektrostatik; Magnetisches Kraftgesetz → Magnetostatik;
Das Coulombsche Gesetz stellt einen Zusammenhang zwischen den elektrischen Größen „Ladung bzw. elektrisches Feld“ und der mechanischen Größe „Kraft“ her. Es ist daher die Basis für den Bau von elektrischen Maschinen.
Mit dem coulombschen Gesetz kann die Kraft zwischen 2 punktförmigen ruhenden Ladungen berechnet werden. Die Kraft die 2 punktförmige Ladungen im Vakuum auf einander ausüben, ist indirekt proportional zum Quadrat des Abstands der beiden Ladungen und direkt proportional zum Produkt der beiden Ladungen. Umgekehrt formuliert nimmt die Kraftwirkung sehr rasch, nämlich quadratisch mit der Entfernung, ab.
Das coulombsche Gesetz gilt für gleich- und ungleichnamige Ladungen. Gleichnamige Ladungen stoßen einander ab, ungleichnamige Ladungen ziehen einander an.
\({F_{12}} = k \cdot \dfrac{{{Q_1} \cdot {Q_2}}}{{{r^2}}} = \dfrac{1}{{4\pi \varepsilon_r {\varepsilon _0}}} \cdot \dfrac{{{Q_1} \cdot {Q_2}}}{{{r^2}}}\)
mit \(\varepsilon = {\varepsilon _0} \cdot {\varepsilon _r}\) und der Coulomb-Konstante \(k = 8,99 \cdot {10^9}\dfrac{{{\text{Vm}}}}{{{\text{As}}}}\)
Beispiel: Überprüfen wir das Coulombsche Gesetz mittels einer Einheitengleichung:
\(\begin{array}{l} {F_C} = \dfrac{1}{{4\pi \cdot {\varepsilon _0} \cdot {\varepsilon _r}}} \cdot \dfrac{{{Q_1} \cdot {Q_2}}}{{{r^2}}}\\ N = \dfrac{1}{{\dfrac{{As}}{{Vm}}}} \cdot \dfrac{{{C^2}}}{{{m^2}}} = \dfrac{{Vm \cdot {C^2}}}{{As \cdot {m^2}}} = \dfrac{{V \cdot {C^2}}}{{As \cdot m}} = \\ {\rm{mit }}C = As = \dfrac{{Nm}}{V} \to V = \dfrac{{Nm}}{C}\\ = \dfrac{{\dfrac{{Nm}}{C} \cdot {C^2}}}{{C \cdot m}} = \dfrac{{Nm \cdot C}}{{C \cdot m}} = N\,\,\,\,{\rm{wzbw}}{\rm{.}} \end{array}\)
Das coulombsche Gesetz gibt ein Maß / eine Formel für jene Kraft an, die 2 punktförmige Ladungen im Vakuum auf einander ausüben und zwar zufolge der fundamentalen elektromagnetischen Wechselwirkung. Der Raum um und zwischen den beiden Ladungen ist von einem elektromagnetischen Feld erfüllt. Das elektrische Feld ist eine Folge des Vorhandenseins von elektrischer Ladung (und einer allfällig zusätzlich vorhandenen zeitlichen Änderung eines Magnetfeldes).
Das Quant / das Boson der fundamentalen elektromagnetischen Wechselwirkung ist das Photon, welches daher der Vermittler der anziehenden oder abstoßenden Kräfte zwischen den beiden punktförmigen Ladungen ist.
Unterschied coulombsche Kraft, Lorentzkraft und elektromagnetische Kraft bzw. Urspannung
Man unterscheidet 3 Arten von Kräften, die auf elektrische Ladungen wirken
- Die coulombsche Kraft wirkt zwischen 2 punktförmigen ruhenden Ladungen, ihre Ursache ist das elektrische Feld. Sie ist daher ein Phänomen der Elektrostatik und bewirkt Spannung zufolge von Potentialunterschieden.
- Die elektromagnetische Kraft (EMK) entspricht der Fähigkeit eines Systems eine Spannung – die „Urspannung“ - zu erzeugen. Konkret ist die Urspannung jene Spannung, die in einem elektrischen Leiter induziert wird, wenn sich der magnetische Fluss durch den Leiter ändert. Es handelt sich dabei um ein Phänomen der Elektrodynamik.
- Die Lorentzkraft wirkt auf bewegte Ladungen im Magnetfeld und ist daher ein Phänomen der Elektrodynamik. Diese Kraft wirkt senkrecht zur Bewegungsrichtung des geladenen Teilchens und senkrecht zur Richtung vom Magnetfeld. Die Lorentzkraft führt dazu, dass sich Elektronen in einem Magnetfeld auf gekrümmten Bahnen bewegen.
Das elektrische Feld
Elektrisches Feld → Elektrostatik; Magnetisches Feld → Magnetostatik;
Sind in einem Raum ruhende oder bewegte elektrische Ladungen Q vorhanden, so verursachen diese Ladungen die Ausbildung eines elektrischen Feldes \(\overrightarrow E \). Zufolge des elektrischen Feldes wirken zwischen gleichnamigen oder ungleichnamigen Ladungen die abstoßende oder anziehende Coulombsche Kraft \(\overrightarrow {{F_C}} \)
Elektrische Feldlinien
Elektrische Feldlinien → Elektrostatik; Magnetische Feldlinien → Magnetostatik;
Alle Ladungen Q sind von einem elektrischen Feld \(\overrightarrow E \) umgeben. Die elektrische Ladung verändert nämlich den umgebenden Raum, indem sie dort ein elektrisches Feld erzeugt.
Elektrische Feldlinien zeigen den Verlauf des Feldes, wobei sie bei positiven Ladungen beginnen und bei negativen Ladungen enden, sich nie schneiden und senkrecht zu den Ladungen stehen. Man spricht daher von einem Quellenfeld. Die positiven Ladungen sind dabei die Quellen, die negativen Ladungen sind die Senken.
Die Dichte der Feldlinien (also wie eng oder weit die Feldlinien auseinander liegen) ist ein Maß für die Feldstärke. Die Feldstärke ist nahe einer Ladung hoch, entsprechend liegen die Feldlinien dicht beieinander und dünnt dann mit zunehmender Entfernung aus. Die Richtung der Coulombschen Kraft auf eine Ladung im Feld wirkt tangential zu den Feldlinien. In einem homogenen Feld liegen die Feldlinien parallel zueinander.
Elektrische Feldstärke
Elektrische Feldstärke → Elektrostatik; Magnetische Feldstärke → Magnetostatik;
Die elektrische Feldstärke \(\overrightarrow E \) ist eine vektorielle Größe, welche die Stärke und die Richtung eines elektrischen Feldes und somit die Fähigkeit des elektrischen Feldes, eine Kraft auf eine darin enthaltene Ladung auszuüben, angibt. Die elektrische Feldstärke entspricht der auf die Längeneinheit der Feldlinie bezogenen Potentialdifferenz. Ihre Ursache sind elektrische Ladungen. Ihre Einheit ist entsprechend Volt pro Meter \(\left[ E \right] = \dfrac{{\text{V}}}{{\text{m}}}\). Die elektrische Feldstärke ist von der Potentialdifferenz, somit also der Spannung (in Volt) und dem Abstand der geladenen Körper (in Meter) abhängig.
\(\vec E = - \dfrac{{\Delta \varphi }}{{\Delta l}}\)
Zwischen zwei benachbarten Potentialflächen muss stets der konstante Potentialwert \(\vartriangle \varphi \) liegen, das bedeutet jedoch noch lange nicht, dass die Potentialflächen auch immer gleich weit voneinander entfernt liegen. Um anzeigen zu können, wo Potentialflächen näher und wo sie weiter voneinander entfernt liegen, wurde die elektrische Feldstärke \(\overrightarrow E \) definiert. Vereinfacht ausgedrückt gibt sie an, wie viele Potentialflächen gerichtet durchstoßen werden, wenn wir in eine bestimmte Richtung um die Wegstrecke \(\Delta l\) weit gehen.
Elektrische Feldstärke einer Punktladung
Die elektrische Feldstärke, die durch eine endliche punktförmig idealisierte Ladung Q ausgeht, nimmt mit dem Quadrat der Entfernung ab. Die Feldlinien stehen radial auf die kugelförmig gedachte Punktladung, die kugelschichtförmig von Äquipotentialflächen umgeben ist.
Die elektrische Feldstärke einer Punktladung Q verläuft radialsymmetrisch. Ihre Stärke nimmt mit 1/r² mit zunehmender Entfernung gemäß folgender Gleichung ab:
\(\left| {\vec E} \right| = \dfrac{1}{{4 \cdot \pi \cdot {\varepsilon _0} \cdot {\varepsilon _r}}} \cdot \dfrac{Q}{{{r^2}}}\)
mit Q als punktförmige Ladung in Coulomb, etwa ein Elektron oder Proton, r als Abstand von der punktförmigen Ladung und \({\varepsilon _0},\,\,{\varepsilon _r}\) als der elektrische Feldkonstante, einer Naturkonstante bzw. Materialkonstante für den vom Feld erfüllten Raum.
Elektrische Flussdichte
Elektrische Flussdichte → Elektrostatik; Magnetische Flussdichte → Magnetostatik;
Die elektrische Flussdichte \(\overrightarrow D \) ist ein vektorielles Maß für die Dichte der elektrischen Feldlinien in Relation zu einer Fläche. Die elektrische Feldstärke \(\overrightarrow E \) ist mit der elektrischen Flussdichte \(\overrightarrow D \) über die elektrische Feldkonstante \(\varepsilon \) verknüpft.
\(\eqalign{ & \overrightarrow D = {\varepsilon _r} \cdot {\varepsilon _0} \cdot \overrightarrow E \cr & \left[ {\overrightarrow D } \right] = \dfrac{{\text{C}}}{{{{\text{m}}^{\text{2}}}}} \cr} \)
Elektrischer Fluss Psi
Elektrische Fluss → Elektrostatik; Magnetische Fluss → Magnetostatik;
Allgemein bezeichnet man jedes Flächenintegral über eine Vektorgröße als Fluss.
Der elektrische Fluss \(\Psi \) (sprich "Psi") ist ein Maß für die Anzahl der elektrischen Feldlinien, die durch ein Flächenelement laufen.
\(\Psi = \iint {\vec D}{\mkern 1mu} {\mkern 1mu} d\vec A = \oint {\vec D{\mkern 1mu} {\mkern 1mu} d\vec A} \)
Zusammenhang elektrische Feldkonstante, magnetische Feldkonstante und Lichtgeschwindigkeit
Die Lichtgeschwindigkeit verknüpft die elektrischer Feldkonstante und magnetischer Feldkonstante wie folgt:
\({c_0} = \dfrac{1}{{\sqrt {{\varepsilon _0} \cdot {\mu _0}} }}\)
Elektrische Feldkonstante (Permittivität)
Elektrische Feldkonstante → Elektrostatik; Magnetische Feldkonstante → Magnetostatik;
Unterschiedliche Materialien haben eine unterschiedliche Durchlässigkeit für elektrische Felder. Das Maß dafür ist die elektrische Feldkonstante bzw. Permittivität \(\varepsilon \) (bzw. veraltet Dielektrizitätskonstante). Die elektrische Durchlässigkeit eines Stoffs \(\varepsilon \) (sprich "Epsilon"), ist das Produkt aus der elektrischen Feldkonstante die im Vakuum \({\varepsilon _0}\) gilt und einem materialspezifischen dimensionslosen Faktor \({\varepsilon _r}\).
\(\begin{array}{l} \varepsilon = {\varepsilon _0} \cdot {\varepsilon _r}\\ \left[ {{\varepsilon _0}} \right] = \left[ \varepsilon \right] = \frac{{As}}{{Vm}}\\ \left[ {{\varepsilon _r}} \right] = 1\\ {\varepsilon _0} = \dfrac{1}{{{c^2} \cdot {\mu _0}}} = 4 \cdot \pi \cdot {10^{ - 7}}\dfrac{{As}}{{Vm}} \end{array}\)
Für das Vakuum gilt:
\({\varepsilon _0} = 8,8542 \cdot {10^{12}}\dfrac{{{\text{As}}}}{{{\text{Vm}}}} = 8,8542 \cdot {10^{12}}\dfrac{F}{m}\)
Da sich Luft nur geringfügig polarisieren lässt, gilt für Luft: \({\varepsilon _r} \approx 1\). Wasser hat eine relative Permittivität von \({\varepsilon _r} \approx 80\). Mit steigender Temperatur nimmt die relative Permittivität ab, was auf die steigende Unordnung der Ladungsträger zurückzuführen ist.
Die relative Permittivität \({\varepsilon _r}\) von Dielektrika ist > 1, jene vom Vakuum ist exakt 1, jene von Leiter ist <1. Die relative Permittivität ist mitunter stark frequenzabhängig.
Schon den nächsten Urlaub geplant?
Auf maths2mind kostenlos auf Prüfungen vorbereiten!
Nach der Prüfung mit dem gesparten Geld deinen Erfolg genießen.

Maßzahl, Größe und Einheit
Physikalische Größen sind das Produkt aus einer Maßzahl mit einer Einheit.
Größe = Maßzahl x Einheit
Maßzahl
Die Maßzahl gibt den Betrag (Menge, Stückzahl,...) als eine konkrete Zahl aus der Menge der reellen Zahlen an.
Basisgröße
Die Größe(nart) legt fest, um welche physikalische Größe es sich handelt. Es gibt sieben voneinander unabhängige Basisgrößen.
Abgeleitete Größe
Aus den sieben von einander unabhängigen Basisgrößen setzen sich alle anderen physikalischen Größen zusammen.
Basiseinheit
Jeder der sieben Basisgrößen ist eine Basiseinheit und ein Einheitenzeichen zugeordnet. Manche Basiseinheiten sind von anderen Basiseinheiten abhängig. So geht etwa in die Definition von der Basiseinheit "Meter" die Basiseinheit "Sekunde" ein. Die Einheit umfasst auch die Zehnerpotenz der Maßzahl. Zum Beispiel für 103 steht Kilo, für 106 steht Mega oder für 10-9 steht nano vor der eigentlichen Einheit.
Einheit
Einheiten dienen dazu Größen zu messen. Für abgeleitete Größen verwendet man Einheiten, die sich aus Basiseinheiten zusammen setzen.
Beispiel:
Zwei Holzstücke mit 7cm bzw. 7m Länge. Diese beiden physikalischen Größen setzen sich zusammen aus
- einer Maßzahl, die den Betrag angibt (in beiden Fällen "7")
- einer Größe(nart), die festlegt um welche Qualität es sich handelt (in beiden Fällen "Länge")
- einer Einheit, die festlegt wie der Betrag abzuzählen ist (im Beispiel "cm" bzw. "m")
Beispiel:
Vergleiche 7m, 7cm
Wir bringen auf die gleiche Einheit "m"
7cm = 0,07m
Nun können wir die Werte an Hand ihrer Zahlenwerte wie folgt vergleichen
7m > 0,07m=7cm
Ein Holzstück von 7m Länge ist länger als ein Holzstück mit einer Länge von 7cm.
7 SI Basisgrößen und ihre Basiseinheiten
Die 7 Basisgrößen sind von einander unabhängige Grundgrößen der Physik. SI steht für „Système international d’unités“, das ist das am weitesten verbreitete internationale Einheitensystem.
| Basisgröße, Formelzeichen | Basiseinheit | Einheitszeichen |
| Länge l | Meter | m |
| Masse m | Kilogramm | kg |
| Zeit t | Sekunde | s |
| elektrische Stromstärke I | Ampere | A |
| Temperatur T | Kelvin | K |
| Stoffmenge n | Mol | mol |
| Lichtstärke Iv | Candela | cd |
SI abgeleitete Größen und ihre Einheiten
Während die 7 Basisgrößen von einander unabhängig sind, haben daraus zusammengesetzte, sogenannte abgeleitete Größen entsprechende abgeleitete Einheiten. Wichtige abgeleitete Größen und ihre Einheiten sind
| Abgeleitete physikalische Größe, Formelzeichen | Einheit | Einheitszeichen |
| Fläche A | Quadratmeter | m² |
| Volumen V | Kubikmeter | m³ |
| Geschwindigkeit v | Kilometer pro Stunde | m/s |
| Beschleunigung a | Meter pro Sekundenquadrat | m/s² |
| mechanische Kraft F | Newton | N |
| Frequenz f | Herz | Hz |
| Arbeit W, Energie E, Wärmemenge Q | Joule | J |
| mechanische Leistung P | Watt | W |
| Druck p | Pascal | Pa |
| Lichtstrom Φ | Lumen | lm |
| Beleuchtungsstärke E | Lux | lx |
SI abgeleitete Größen und ihre Einheiten aus der Elektrotechnik
Während die 7 Basisgrößen von einander unabhängig sind, haben daraus zusammengesetzte, sogenannte abgeleitete Größen entsprechende abgeleitete Einheiten. Wichtige abgeleitete Größen und ihre Einheiten aus dem Gebiet der Elektrotechnik sind
| Abgeleitete elektrotechnische Größe, Formelzeichen | Einheit | Einheitszeichen |
| magnetische Feldstärke \({\overrightarrow H }\) | Ampere pro m | A/m |
| elektrische Feldstärke \({\overrightarrow E }\) | Volt pro m | V/m |
| Spannung U | Volt | V |
| Arbeit W, Energie E | Joule | J |
| elektrische Ladung Q | Coulomb | C |
| elektrische Leistung P | Watt | W |
| ohmscher Widerstand R | Ohm | \(\Omega\) |
| elektrische Kapazität C | Farad | F |
| magnetische Induktivität L | Henry | H |
| magnetischer Fluss \(\Phi\) | Weber | Wb |
| magnetische Flussdichte \({\overrightarrow B }\) | Tesla | T |
Physikalische Größen - Auswahl und Definition gemäß Formelsammlung AHS
| Größe | Formel | Formel | Formel |
| Dichte ρ | \(\rho = \dfrac{m}{v}\) | ||
| Leistung P | \(P = \dfrac{{\Delta E}}{{\Delta t}}\) | \(P = \dfrac{{\Delta W}}{{\Delta t}}\) | \(P = \dfrac{{dW\left( t \right)}}{{dt}}\) |
| Kraft F | \(F = m \cdot a\) | \(F = \dfrac{{dW}}{{ds}}\) | |
| Arbeit | \(W = F \cdot s\) | \(W = \int {F\left( s \right)\,\,\operatorname{ds} }\) | |
| kinetische Energie Ekin | \({E_{kin}} = \dfrac{{m \cdot {v^2}}}{2}\) | ||
| potentielle Energie Epot | \({E_{pot}} = m \cdot g \cdot h\) | ||
| gleichförmige geradlinige Bewegung v(t) | \(v = \dfrac{s}{t}\) | \(v = \dfrac{{ds}}{{dt}}\) | \(v\left( t \right) = s'\left( t \right) = \dfrac{{ds}}{{dt}}\) |
| gleichmäßig beschleunigte geradlinige Bewegung a(t) | \(v = a \cdot t + {v_0}\) | \(a = \dfrac{{dv}}{{dt}}\) | \(a\left( t \right) = v'\left( t \right) = \dfrac{{dv}}{{dt}} = s''\left( t \right) = \dfrac{{{d^2}s}}{{d{t^2}}}\) |
Bewegungsvorgänge - Auswahl und Definition gemäß Formelsammlung BHS
| Größe | Formel |
| Zeit t | \(t\) |
| Weg-Zeit-Funktion s(t) | \(s\left( t \right) = \int {v\left( t \right)} \,\,dt\) |
| Geschwindigkeit-Zeit-Funktion v(t) | \(v(t) = s'\left( t \right) = \mathop s\limits^ \bullet = \dfrac{{ds}}{{dt}} = \int {a\left( t \right)} \,\,dt\) |
| Beschleunigung-Zeit-Funktion a(t) | \(a\left( t \right) = s''\left( t \right) = \mathop s\limits^{ \bullet \bullet } = \dfrac{{{d^2}s}}{{d{t^2}}} = v'\left( t \right) = \mathop v\limits^ \bullet = \dfrac{{dv}}{{dt}}\) |
Anmerkung zur auf Universitäten üblichen Kurzschreibweise von "Ableitungen nach der Zeit": Die Notation mit einem "Punkt" über dem Formelzeichen bedeutet, dass es sich um die 1 Ableitung nach der Zeit handelt. Zwei "Punkte" bedeuten, dass es sich um die 2. Ableitung nach der Zeit handelt.
Größen und ihre Einheiten - Auswahl gemäß Formelsammlung AHS
| Größe | Einheit | Symbol | Beziehung zu SI-Einheiten |
| Temperatur T | Grad Celsius Grad Kelvin |
°C K |
\(\Delta t = \Delta T\) |
| Frequenz f | Hertz | Hz | \(1 \cdot Hz = 1 \cdot {s^{ - 1}}\) |
| Arbeit W, Energie E, Wärmemenge Q | Joule | J | \(1 \cdot J = 1 \cdot kg \cdot {m^{2}}\cdot s^{ - 2}\) |
| Kraft F | Newton | N | \(1 \cdot N = 1 \cdot kg \cdot m \cdot {s^{ - 2}}\) |
| Drehmoment M | Newtonmeter | \(N \cdot m\) | \(1 \cdot N \cdot m = 1 \cdot kg \cdot {m^2} \cdot {s^{ - 2}}\) |
| Elektrischer Widerstand R | Ohm | \(\Omega\) | \(1 \cdot \Omega = 1 \cdot V \cdot {A^{ - 1}} = 1 \cdot kg \cdot {m^2} \cdot {A^{ - 2}} \cdot {s^{ - 3}}\) |
| Druck p | Pascal | Pa | \(1 \cdot Pa = 1 \cdot N \cdot {m^{ - 2}} = 1 \cdot kg \cdot {m^{ - 1}} \cdot {s^{ - 2}}\) |
| Elektrische Stromstärke I | Ampere | A | \(1 \cdot A = 1 \cdot C \cdot {s^{ - 1}}\) |
| Elektrische Spannung U | Volt | V | \(1 \cdot V = 1 \cdot J \cdot {C^{ - 1}} = 1 \cdot kg \cdot {m^2} \cdot {A^{ - 1}} \cdot {s^{ - 3}}\) |
| Leistung P | Watt | W | \(1 \cdot W = 1 \cdot J \cdot {s^{ - 1}} = 1 \cdot kg \cdot {m^2} \cdot {s^{ - 3}}\) |