Tesla (Einheit magnetischen Flussdichte)
Hier findest du folgende Inhalte
Formeln
Vorab eine Mindmap zu den Inhalten dieser Mikro-Lerneinheit
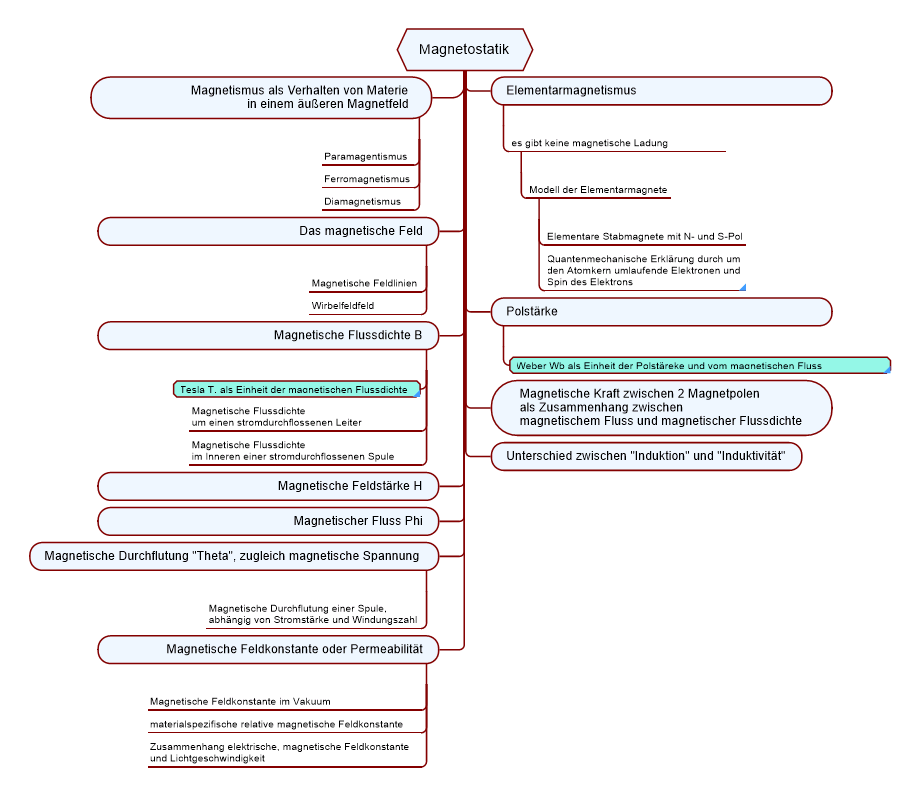
Magnetostatik
Die Magnetostatik ist der einfachste Fall der Elektrodynamik. Sie beschreibt die Felder, die einen von einem zeitunabhängigen Strom (=Gleichstrom) durchflossenen Leiter umgeben, sowie die Kräfte, die zwischen Magnetpolen wirken.
Elementarmagnetismus
Elementarmagnetismus → Magnetostatik; Elektrische Elementarladung → Elektrostatik;
In der Natur gibt zwar die elektrische Elementarladung e aber es gibt keine „magnetische Ladung“. Daher gibt es auch keine magnetischen Monopole, das wären isoliert existierende Nord- oder Südpole. Magnetisch Felder besitzen somit im Unterschied zu elektrischen Feldern keine Quellen (Anfang einer Feldlinie) bzw. Senken (Ende einer Feldlinie), sondern sie sind Wirbelfelder, mit geschlossenen oder sich ins Unedliche windenden Feldlinien. Daher lautet in der Elektrodynamik die 2. Maxwellgleichung, also das Gaußsche Gesetz für magnetische Felder \(div\overrightarrow B = 0\)
Um die magnetischen Eigenschaften von Materie zu erklären verwendet man das Modell der „Elementarmagnete“. Elementarmagnete sind die kleinste magnetische Einheit in einem ferromagnetischen Material. Jedes Atom kann als kleinster isolierbarer Elementarmagnet betrachtet werden, da es ein magnetisches Moment besitzt, welches durch die in der Elektronenhülle umlaufenden und sich dabei drehenden (Spin) Elektronen verursacht werden. Umlaufende Elektronen entsprechen einem Stromfluss, jeder fließende Strom erzeugt ein Magnetfeld.
- Elementare Stabmagnete (als einfache Erklärung): Vereinfacht kann man sich einen Magneten als Ansammlung von elementaren Stabmagneten vorstellen. Jeder Elementarmagnet besitzt einen N-Pol und einen S-Pol und ist frei drehbar. Die Anordnung hängt vom Kristallgitter ab. Bei ferromagnetischen Stoffen führt die gegenseitige Wechselwirkung zu einer Ausrichtung aller Elementarmagnete innerhalb eines sogenannten Weiss’schen Bezirks in die gleiche Richtung.
Ob das magnetische Moment der einzelnen Atome (Elementarmagnete) sich lokal aufhebt oder makroskopisch wirksam wird, hängt von der jeweiligen Anordnung der Atome in der betrachteten Kristallstruktur ab. - Quantenmechanische Erklärung: Wenn - gedanklich - die negativ geladenen Elektronen um den Atomkern umlaufen, so entspricht dies einem Stromfluss um den Kern, der die Ursache für ein Magnetfeld ist. Auch durch die - gedankliche - Eigendrehung des Elektrons (Spin) entsteht ein Beitrag zum magnetischen Dipolmoment.
Ob ein Atom auf Grund der Bahnbewegung und durch den Spin der Elektronen ein magnetisches Moment besitzt, hängt von der Anzahl der Elektronen im Atom und somit vom jeweiligen chemischen Element ab.
Magnetismus als Verhalten von Materie in einem äußeren Magnetfeld
Paramagnetismus
Man spricht vom „Paramagnetismus“ wenn sich die Elementarmagnete unter der Wirkung eines äußeren Magnetfelds so ausrichten, dass sie dieses verstärken. Die Magnetisierung ist dabei proportional zum angelegten Magnetfeld. Paramagnetische Stoffe werden durch ein äußeres Magnetfeld schwach angezogen.
Ferromagnetismus
Von „Ferromagnetismus“ spricht man, wenn sich in kleinen Bereichen des Körpers - in den „Weiß’schen Bezirken“ - die Spins auch ohne äußeres Magnetfeld parallel ausrichten. Da die Spinns benachbarter Bezirke verschieden orientiert sind, hat der Ferromagnet keine makroskopische Magnetisierung. Ferromagnetische Stoffe (bei Raumtemperatur: Eisen, Nickel und Kobalt) werden vom äußeren Magnetfeld stark angezogen. Bei hohen Temperaturen werden ferromagnetische Stoffe paramagnetisch.
Ferromagnetische Stoffe können Magnete bilden, etwa kostengünstige Ferrit Magnete aus Eisenoxid. Sie sind aber nur in Form von Legierungen (z.B.: NdFeB – Neodym, AlNiCo – Aluminium + Nickel + Kobalt, SmCo – Samarium-Kobalt) als Dauermagnete geeignet.
Diamagnetismus
Von „Diamagnetismus“ spricht man, wenn ein äußeres magnetischen Feld \( \overrightarrow H\) auf Materie wirkt, und in jedem Atom ein Kreisstrom induziert wird, dessen magnetisches Moment gemäß der Lenz’schen Regel, dem von außen angelegten Feld entgegengesetzt ist. Diamagnetische Stoffe werden vom äußeren Magnetfeld schwach abgestoßen.
Polstärke
Polstärke → Magnetostatik; Elektrische Ladung → Elektrostatik;
So wie es in der Elektrostatik positive +e und negative Ladungen -e gibt, wo einander gleichnamige Ladungen abstoßen, während sich ungleichnamige Ladungen anziehen, gibt es in der Magnetostatik zwei verschiedene Pole, den Nordpol und den Südpol, wo einander gleichnamige Magnetpole abstoßen, während sich ungleichnamige Magnetpole anziehen. Während man positive und negative elektrische Ladungen trennen kann, kann man Nord- und Südpol eines Magneten nicht trennen. Jeder noch so kleine Magnet hat grundsätzlich immer sowohl N- als auch S-Pol. Man könnte daher formulieren, dass die Polstärke die „scheinbare“ magnetische Ladung eines Magnetpols angibt. Tatsächlich wird sie durch den magnetischen Fluss \(\Phi \)gemessen, der von einem Magnetpol ausgeht und durch eine Fläche fließt.
Die Polstärke \(\overrightarrow p \) gibt die Stärke und die Orientierung der beiden Pole eines Magneten an.
Weber
Weber → Magnetostatik; Coulomb → Elektrostatik;
Das Weber Wb ist die Einheit der magnetischen Polstärke bzw. vom magnetischen Fluss. Da es keine räumlich isolierten magnetischen Monopole gibt, wird die Polstärke durch den magnetischen Fluss \(\Phi \) gemessen, der von einem Magnetpol ausgeht und durch eine Fläche fließt.
1 Weber Wb ist der magnetische Fluss, der in einer Leiterschleife von 1 m², bei konstanter zeitlicher Änderung des Flusses innerhalb von 1 Sekunde eine Spannung von 1 Volt induziert.
Die Einheit der magnetischen Polstärke, bzw. vom magnetischen Fluss ergibt sich gemäß folgender Einheitengleichung
\(\left[ \Phi \right]{\rm{ = }}\left[ V \right] \cdot \left[ {\rm{t}} \right]{\rm{ = 1V}} \cdot {\rm{1s = 1Vs = 1Wb = 1T}} \cdot {{\rm{m}}^2}\)
Magentische Kraft zwischen zwei Magnetpolen
Magnetisches Kraftgesetz → Magnetostatik; Coulombsches Gesetz → Elektrostatik;
Das Magnetische Kraftgesetz stellt einen Zusammenhang zwischen der magnetischen Größe „Fluss“ bzw. magnetische Flussdichte B“ und der mechanischen Größe „Kraft“ her. Man kann daher analog zum Coulombschen Gesetz das Magnetische Kraftgesetz wie folgt anschreiben
\(F = \dfrac{1}{{4\pi {\mu _0}}} \cdot \dfrac{{{\Phi _1} \cdot {\Phi _2}}}{{{r^2}}} = \dfrac{1}{{4\pi {\mu _0}}} \cdot \dfrac{{{B_1} \cdot {A_1} \cdot {\Phi _2} \cdot {A_2}}}{{{r^2}}} = k \cdot \dfrac{{{p_1} \cdot {p_2}}}{{{r^2}}}\)
Beispiel: Überprüfen wir das Magnetische Kraftgesetz mittels einer Einheitengleichung:
\(\begin{array}{l} F = \dfrac{1}{{4\pi {\mu _0}}} \cdot \dfrac{{{\Phi _1} \cdot {\Phi _2}}}{{{r^2}}} = \dfrac{1}{{4\pi {\mu _0}}} \cdot \dfrac{{{B_1} \cdot {A_1} \cdot {\Phi _2} \cdot {A_2}}}{{{r^2}}}\\ N = \dfrac{1}{{\frac{{Vs}}{{Am}}}} \cdot \dfrac{{W{b^2}}}{{{m^2}}} = \dfrac{{Am \cdot W{b^2}}}{{Vs \cdot {m^2}}} = \dfrac{{A \cdot W{b^2}}}{{Vs \cdot m}} = \\ \\ {\rm{mit Wb}} = Vs = \dfrac{{Nm}}{A} \to V = \dfrac{{Nm}}{{As}}\\ = \dfrac{{A \cdot \dfrac{{{N^2} \cdot {m^2}}}{{{A^2}}}}}{{\dfrac{{Nm}}{{As}} \cdot s \cdot m}} = \dfrac{{A \cdot {N^2} \cdot {m^2} \cdot A \cdot s}}{{{A^2} \cdot N \cdot s \cdot {m^2}}} = N\,\,\,\,{\rm{wzbw}}{\rm{.}} \end{array}\)
Das Magentische Kraftgesetz gibt ein Maß / eine Formel für jene Kraft an, die 2 magnetische Pole auf einander ausüben und zwar zufolge der magnetischen Polstärke. Der Raum zwischen den Polen ist von einem elektromagnetischen Feld erfüllt. Das magnetische Feld ist eine Folge der subatomaren Bewegung von Elektronen auf deren Umlauf um den Atomkern.
Das Quant / das Boson der fundamentalen elektromagnetischen Wechselwirkung ist das Photon, welches daher der Vermittler der anziehenden oder abstoßenden Kräfte zwischen den beiden Magnetpolen ist.
Das magnetische Feld
Magnetisches Feld → Magnetostatik; Elektrisches Feld → Elektrostatik;
Sind in einem Raum bewegte elektrische Ladungen vorhanden, so verursachen diese bewegten Ladungen die Ausbildung eines magnetischen Feldes \(\overrightarrow H\). In Dauermagneten fließen diese das Magnetfeld verursachenden Ströme in Form von bewegten Elektronen auf atomarer Ebene. Das Erdmagnetfeld wird durch die Bewegung von flüssiger leitfähiger Metallschmelze im Erdkern, in einem natürlich vorhandenem Initialfeld, induziert. Zufolge des magnetischen Feldes wirkt auf bewegte geladene Teilchen die sogenannte Lorentzkraft FL.
Magnetische Feldlinien
Magnetische Feldlinien → Magnetostatik; Elektrische Feldlinien → Elektrostatik;
Magnete und bewegte elektrische Ladungen, etwa in Form eines stromdurchflossenen Leiters, sind von einem magnetischen Feld \(\overrightarrow H \) umgeben. Stromfluss verändert nämlich den umgebenden Raum, indem er dort ein magnetisches Feld erzeugt.
Magnetische Feldlinien zeigen den Verlauf des Feldes, wobei magnetische Feldlinien immer geschlossen sind oder sich winden sich unendlich, ohne in sich zurückzulaufen, man spricht daher von einem sogenannten Wirbelfeld. Es gibt keine offenen - also nur geschlossene - magnetischen Feldlinien, weil ein Wirbelfeld keine Quellen und keine Senken hat. Magnetische Feldlinien verlaufen in Richtung vom Nord- zum Südpol.
Die Dichte der Feldlinien (also wie eng oder weit die Feldlinien auseinander liegen) ist ein Maß für die Feldstärke.
Magnetische Feldstärke
Magnetische Feldstärke → Magnetostatik; Elektrische Feldstärke → Elektrostatik;
Die magnetische Feldstärke \(\overrightarrow H\) oder auch magnetische Erregung genannt, ist eine vektorielle Größe, welche die Stärke und die Richtung eines magnetischen Feldes und somit die Fähigkeit des magnetischen Feldes, eine Kraft auf einen darin enthaltenen magnetischen Pol auszuüben, angibt. Ihre Ursache sind elektrische Ströme. Ihre Einheit ist Ampere pro Meter \(\left[ H \right] = \dfrac{A}{m}\). Die magnetische Feldstärke entspricht der magnetischen Spannung Um, bzw. der magnetischen Durchflutung Theta, beide in Ampere A, bezogen auf die Wegeinheit l.
\(\overrightarrow H = \dfrac{{\Delta {U_m}}}{{\Delta l}} = \dfrac{{\Delta \Theta }}{{\Delta l}}\)
Magnetische Flussdichte
Magnetische Flussdichte → Magnetostatik; Elektrische Flussdichte → Elektrostatik;
Die magnetische Flussdichte \({\overrightarrow B }\), auch magnetische Induktion genannt, ist ein vektorielles Maß für die örtliche Intensität des Magnetfeldes, zufolge einer magnetischen Feldstärke \( \overrightarrow H\) . Die beiden Größen sind im Vakuum über die magnetische Feldkonstante \({\mu _0}\) verknüpft. Die magnetische Feldkonstante \(\mu={\mu _r} \cdot {\mu _0}\) ist ein Maß für die Durchlässigkeit eines Materials für magnetische Felder.
\(\begin{array}{l} \overrightarrow B = {\mu _r} \cdot {\mu _0} \cdot \overrightarrow H \\ \left[ {\overrightarrow B } \right] = \dfrac{{{\rm{Vs}}}}{{{\rm{A}} \cdot {\rm{m}}}} \cdot \dfrac{{\rm{A}}}{{\rm{m}}}{\rm{ = }}\dfrac{{{\rm{Wb}}}}{{{{\rm{m}}^{\rm{2}}}}}{\rm{ = }}\dfrac{{\rm{N}}}{{{\rm{A}} \cdot {\rm{m}}}}{\rm{ = T}} \end{array}\)
mit:
\({\mu _0} = 4\pi \cdot {10^{ - 7}}\dfrac{{Vs}}{{Am}}\)
Die magnetische Flussdichte \({\overrightarrow B }\) ist ein auf den Querschnitt bezogener Fluss \(\vec B = \dfrac{{d{\rm{\Phi }}}}{{dA}}\) und erlaubt im Gegensatz zum querschnittsabhängigen Fluss \(\Phi \) eine Exklusivaussage über die herrschende Feldstärke.
Magnetische Flussdichte B um einen stromdurchflossenen Leiter
Fließt durch einen unendlich langen geraden Leiter ein Strom der Stärke I, so ergibt sich der Betrag der magnetischen Flussdichte B im Abstand r vom Leiter wie folgt:
\(B = {\mu _0} \cdot \dfrac{1}{{2\pi r}} \cdot I\)
Die Feldlinien des Magnetfeldes verlaufen dabei in konzentrischen Kreisen senkrecht zum stromdurchflossenen Leiter.
Magnetische Flussdichte B im Inneren einer stromdurchflossenen Spule
\(\overrightarrow B = \dfrac{{n \cdot {\mu _0} \cdot I}}{{{l_{Spule}}}}\)
bzw. wenn die Spule einen Kern hat:
\(\overrightarrow B = \dfrac{{n \cdot {\mu _r} \cdot {\mu _0} \cdot I}}{{{l_{Spule}}}}\)
Tesla (T)
Das Tesla T ist die Einheit der magnetischen Flussdichte. Einem Tesla entspricht jene magnetische Flussdichte, die auf einen 1m langen Leiter, der von einem Strom von 1 A durchflossen wird, eine Kraft von 1 N ausübt. 1 T ist eine sehr große Einheit.
\(\left[ {1 \cdot T = 1 \cdot \dfrac{{V \cdot s}}{{{m^2}}} = 1 \cdot \dfrac{N}{{A \cdot m}} = 1 \cdot \dfrac{{Wb}}{{{m^2}}} = 1 \cdot \dfrac{{kg}}{{A \cdot {s^2}}}} \right]\)
- Das Erdmagnetfeld beträgt ca \(4 \cdot {10^{ - 5}}T\).
- In der Magnetresonanztomographie, einem bildgebenden Verfahren zur Darstellung der Gewebestruktur, erzeugt ein 34 Tonnen Magnet mit 270 Tonnen Eisen zur Abschirmung bis zu 7 Tesla.
Unterschied zwischen Induktion B und Induktivität L
Die magnetische Flussdichte B wird manchmal auch magnetische Induktion genannt. Da "Induktion" und "Induktivität" auf Grund der gemeinsamen ersten 7 Buchstaben sehr ähnlich klingen, sei hier auf den Unterschied hingewiesen.
- Magnetische Flussdichte B - sie wird auch magnetische Induktion genannt - ist ein Maß dafür, wie stark ein Magnetfeld ist. Ihre Einheit ist das Tesla.
- Induktivität L ist eine Eigenschaft einer Spule und hängt nur von deren geometrischer Bauform ab. Ihre Einheit ist das Henry.
Magnetischer Fluss Phi
Magnetische Fluss → Magnetostatik; Elektrische Fluss → Elektrostatik;
Allgemein bezeichnet man jedes Flächenintegral über eine Vektorgröße als Fluss. Der magnetische Fluss \(\Phi\) (sprich: “Phi“) mit der Einheit Weber, ist ein Maß dafür, wie viel Feld \(\overrightarrow B\) etwa aus dem N-Pol eines Magneten austritt. Er gibt die Gesamtzahl aller Feldlinien an, die von einer Spule erzeugt werden.
\(\begin{array}{l} \Phi = \int\limits_A {\overrightarrow B \,\,d\overrightarrow A } \\ \left[ \Phi \right] = Wb \end{array}\)
Der magnetische Fluss \(\Phi\) ist ein Skalar. Der magnetische Fluss ist nur für eine Fläche im Raum definiert, daher auch das Flächenintegral, nicht aber für jeden einzelnen Punkt im Raum. In der Praxis wird daher selten mit dem magnetischen Fluss, sondern mit der magnetischen Flussdichte B gearbeitet.
- Im inhomogenen Feld ergibt sich der magnetische Fluss \(\Phi\), wenn man die magnetische Flussdichte \(\overrightarrow B\) über den Querschnitt \(\overrightarrow A\) aufsummiert (aufintegriert).
- Im homogenen Feld ist der magnetische Fluss \(\Phi\) das „in-Produkt“ aus Felddichte \(\overrightarrow B\) und orientiertem Querschnitt \(\overrightarrow A\) gemäß: \(\Phi = \overrightarrow B \cdot \overrightarrow A \cdot \cos \left( {\angle \overrightarrow B ,\overrightarrow A } \right)\). Der magnetische Fluss hat sein Maximum wenn \(\overrightarrow B \parallel \overrightarrow A\)
Der magnetische Fluss \(\Phi\) ist - vergleichbar zur elektrischen Stromstärke I - die Wirkung einer magnetischen Spannung Um und fließt durch einen materialabhängigen magnetischen Widerstand Rm.
Nachfolgende Gleichung liefert den Zusammenhang zwischen magnetischem Fluss Phi und magnetischer Durchflutung Theta:
\(\Phi = \dfrac{{{U_m}}}{{{R_m}}} = \dfrac{\Theta }{{{R_m}}}\)
Magnetische Durchflutung Theta, zugleich magnetische Spannung Um
Die magnetische Durchflutung \(\Theta\) dient zur Berechnung einer, durch einen elektrischen Storm erzeugten, magnetischen Feldstärke.
\(\Theta = \sum\limits_k {{I_k}} = \int\limits_A {\overrightarrow S \,\,d\overrightarrow A } = {U_m}\)
Die magnetische Durchflutung einer Spule ergibt sich aus Strom mal Windungszahl.
\(\Theta = I \cdot n\)
Die Einheit der magnetischen Durchflutung ist das Ampere bzw. die Amperewindungen.
Eine Spule mit 600 Windungen übt bei einem Strom von 2A eine gleich große Kraft auf ein Eisenstück aus, wie eine Spule mit 1200 Windungen und einem Strom von 1A. Die Windungszahl n hat als Einheit 1.
Die magnetische Durchflutung \(\Theta \) bzw die magnetische Spannung, ist die Ursache für das Vorhandensein einer magnetischen Feldstärke H.
Der nachfolgende Zusammenhang wird Durchflutungssatz genannt und in der Mikro-Lerneinheit „Elektrodynamik“ näher besprochen
\(\Theta = {U_m} = \mathop \oint \limits_s \vec H{\mkern 1mu} {\mkern 1mu} d\vec s = \mathop \smallint \limits_A \vec S{\mkern 1mu} {\mkern 1mu} d\vec A = \mathop \sum \limits_k {I_k}\)
Zusammenhang elektrische Feldkonstante, magnetische Feldkonstante und Lichtgeschwindigkeit
Die Lichtgeschwindigkeit verknüpft die elektrischer Feldkonstante und magnetischer Feldkonstante wie folgt:
\({c_0} = \dfrac{1}{{\sqrt {{\varepsilon _0} \cdot {\mu _0}} }}\)
Magnetische Feldkonstante Mü
Magnetische Feldkonstante → Magnetostatik; Elektrische Feldkonstante → Elektrostatik;
Unterschiedliche Materialien haben eine unterschiedliche Durchlässigkeit für magnetische Felder. Das Maß dafür ist die magnetische Feldkonstante bzw. Permeabilität \({\mu}\). Die magnetische Durchlässigkeit eines Stoffs \({\mu}\) (sprich: „Mü“), ist das Produkt aus der magnetischen Feldkonstante die im Vakuum gilt \({\mu _0}\) und einem materialspezifischen dimensionslosen Faktor \({\mu _r}\)
Für Luft ist \({\mu _r} \approx 1\). Luft und Vakuum leiten daher sehr schlecht. Ferromagnetische Stoffe hingegen haben eine hohe magnetische Durchlässigkeit \({\mu _{r,\,Fe}} \approx 200\). D.h. die magnetischen Kraftlinien schließen sich bevorzugt über Eisenwege und nur kleine Streuanteile gehen über Luft. Die magnetische Leitfähigkeit von CU: \({\mu _{r,\,Cu}} \approx 1\)
\(\eqalign{ & \mu = {\mu _r} \cdot {\mu _0} \cr & \left[ \mu \right] = \dfrac{{Vs}}{{Am}} \cr & \left[ {{\mu _r}} \right] = 1 \cr & {\mu _0} = \dfrac{1}{{{\varepsilon _0} \cdot {c^2}}} = 4 \cdot \pi \cdot {10^{ - 7}}\dfrac{{Vs}}{{Am}} \cr} \)
Materialien unterscheiden sich erheblich bezüglich ihrer relativen Permeabilität. Diamagnetische Stoffe besitzen eine relative Permeabilität zwischen 0 und 1. Ein Supraleiter 1. Art verdrängt ein von außen vorhandenes Magnetfeld vollständig aus seinem Inneren und hat daher \({\mu _{r,Supraleiter}} = 0\). Für Wasser und Luft gilt: \({\mu _{r,H2O}} = 0,999991;\,\,\,\,\,{\mu _{r,Luft}} = 1,0000004\). Für Eisen gilt der Bereich \({\mu _{r,Eisen}} \approx 300...10000\). Für amorphe oder nanokristalline Metalle liegt die relative Permeabilität bei Werten bis einige Hundertausend.
Um eine bestimmte magnetische Induktion L etwa in Eisen hervorzurufen, bedarf es zufolge \(\overrightarrow B = \mu \cdot \overrightarrow H\) einer weit geringeren magnetischen Feldstärke \( \overrightarrow H\) , als etwa für die gleiche magnetische Induktion L in Luft erforderlich wäre. Wenn allerdings im Eisen alle Elementarmagnete ausgerichtet sind, d.h. im Bereich sehr hoher Sättigung, ist die Zunahme der magnetischen Flussdichte \(\overrightarrow B\) bei weiterer Steigerung der äußeren magnetischen Feldstärke \(\overrightarrow H\) schließlich nicht mehr größer als in Luft.
Rechnenbeispiel zum Zusammenhang: magn. Durchflutung, magn. Feldstärke und magn. Flussdichte
Eine Spule mit n=5000 Windungen wird von einem Strom I=10mA durchflossen.
1. Teilaufgabe
Wie groß ist die magnetische Durchflutung der Spule?
\(\Theta = \sum\limits_k {{I_k}} \)
\(\Theta = I \cdot n = \left( {10 \cdot {{10}^{ - 3}}} \right) \cdot \left( {5 \cdot {{10}^3}} \right) = 50A\)
Die Länge einer mittleren Feldlinie beträgt 20cm.
2. Teilaufgabe
Wie groß ist die magnetische Feldstärke?
\(H = \dfrac{\Theta }{{{l_{Mittel}}}} = \dfrac{{50A}}{{0,2m}} = 250\frac{A}{m}\)
Bei der Spule handle es sich um eine Luftspule mit \({\mu _r} = 1\)
3. Teilaufgabe
Wie groß ist die magnetische Flussdichte?
\(B = {\mu _0} \cdot {\mu _r} \cdot H = 4 \cdot \pi \cdot {10^{ - 7}} \cdot 1 \cdot 250 \approx 0,314mT\)
In die Luftspule wird ein Eisenkern mit \({\mu _r} = 6000\) eingebracht.
4. Teilaufgabe
Wie groß ist die magnetische Flussdichte?
\(B = {\mu _0} \cdot {\mu _r} \cdot H = 4 \cdot \pi \cdot {10^{ - 7}} \cdot 6000 \cdot 250 \approx 1,885T\)
Schon den nächsten Urlaub geplant?
Auf maths2mind kostenlos auf Prüfungen vorbereiten!
Nach der Prüfung mit dem gesparten Geld deinen Erfolg genießen.

Maßzahl, Größe und Einheit
Physikalische Größen sind das Produkt aus einer Maßzahl mit einer Einheit.
Größe = Maßzahl x Einheit
Maßzahl
Die Maßzahl gibt den Betrag (Menge, Stückzahl,...) als eine konkrete Zahl aus der Menge der reellen Zahlen an.
Basisgröße
Die Größe(nart) legt fest, um welche physikalische Größe es sich handelt. Es gibt sieben voneinander unabhängige Basisgrößen.
Abgeleitete Größe
Aus den sieben von einander unabhängigen Basisgrößen setzen sich alle anderen physikalischen Größen zusammen.
Basiseinheit
Jeder der sieben Basisgrößen ist eine Basiseinheit und ein Einheitenzeichen zugeordnet. Manche Basiseinheiten sind von anderen Basiseinheiten abhängig. So geht etwa in die Definition von der Basiseinheit "Meter" die Basiseinheit "Sekunde" ein. Die Einheit umfasst auch die Zehnerpotenz der Maßzahl. Zum Beispiel für 103 steht Kilo, für 106 steht Mega oder für 10-9 steht nano vor der eigentlichen Einheit.
Einheit
Einheiten dienen dazu Größen zu messen. Für abgeleitete Größen verwendet man Einheiten, die sich aus Basiseinheiten zusammen setzen.
Beispiel:
Zwei Holzstücke mit 7cm bzw. 7m Länge. Diese beiden physikalischen Größen setzen sich zusammen aus
- einer Maßzahl, die den Betrag angibt (in beiden Fällen "7")
- einer Größe(nart), die festlegt um welche Qualität es sich handelt (in beiden Fällen "Länge")
- einer Einheit, die festlegt wie der Betrag abzuzählen ist (im Beispiel "cm" bzw. "m")
Beispiel:
Vergleiche 7m, 7cm
Wir bringen auf die gleiche Einheit "m"
7cm = 0,07m
Nun können wir die Werte an Hand ihrer Zahlenwerte wie folgt vergleichen
7m > 0,07m=7cm
Ein Holzstück von 7m Länge ist länger als ein Holzstück mit einer Länge von 7cm.
7 SI Basisgrößen und ihre Basiseinheiten
Die 7 Basisgrößen sind von einander unabhängige Grundgrößen der Physik. SI steht für „Système international d’unités“, das ist das am weitesten verbreitete internationale Einheitensystem.
| Basisgröße, Formelzeichen | Basiseinheit | Einheitszeichen |
| Länge l | Meter | m |
| Masse m | Kilogramm | kg |
| Zeit t | Sekunde | s |
| elektrische Stromstärke I | Ampere | A |
| Temperatur T | Kelvin | K |
| Stoffmenge n | Mol | mol |
| Lichtstärke Iv | Candela | cd |
SI abgeleitete Größen und ihre Einheiten
Während die 7 Basisgrößen von einander unabhängig sind, haben daraus zusammengesetzte, sogenannte abgeleitete Größen entsprechende abgeleitete Einheiten. Wichtige abgeleitete Größen und ihre Einheiten sind
| Abgeleitete physikalische Größe, Formelzeichen | Einheit | Einheitszeichen |
| Fläche A | Quadratmeter | m² |
| Volumen V | Kubikmeter | m³ |
| Geschwindigkeit v | Kilometer pro Stunde | m/s |
| Beschleunigung a | Meter pro Sekundenquadrat | m/s² |
| mechanische Kraft F | Newton | N |
| Frequenz f | Herz | Hz |
| Arbeit W, Energie E, Wärmemenge Q | Joule | J |
| mechanische Leistung P | Watt | W |
| Druck p | Pascal | Pa |
| Lichtstrom Φ | Lumen | lm |
| Beleuchtungsstärke E | Lux | lx |
SI abgeleitete Größen und ihre Einheiten aus der Elektrotechnik
Während die 7 Basisgrößen von einander unabhängig sind, haben daraus zusammengesetzte, sogenannte abgeleitete Größen entsprechende abgeleitete Einheiten. Wichtige abgeleitete Größen und ihre Einheiten aus dem Gebiet der Elektrotechnik sind
| Abgeleitete elektrotechnische Größe, Formelzeichen | Einheit | Einheitszeichen |
| magnetische Feldstärke \({\overrightarrow H }\) | Ampere pro m | A/m |
| elektrische Feldstärke \({\overrightarrow E }\) | Volt pro m | V/m |
| Spannung U | Volt | V |
| Arbeit W, Energie E | Joule | J |
| elektrische Ladung Q | Coulomb | C |
| elektrische Leistung P | Watt | W |
| ohmscher Widerstand R | Ohm | \(\Omega\) |
| elektrische Kapazität C | Farad | F |
| magnetische Induktivität L | Henry | H |
| magnetischer Fluss \(\Phi\) | Weber | Wb |
| magnetische Flussdichte \({\overrightarrow B }\) | Tesla | T |
Physikalische Größen - Auswahl und Definition gemäß Formelsammlung AHS
| Größe | Formel | Formel | Formel |
| Dichte ρ | \(\rho = \dfrac{m}{v}\) | ||
| Leistung P | \(P = \dfrac{{\Delta E}}{{\Delta t}}\) | \(P = \dfrac{{\Delta W}}{{\Delta t}}\) | \(P = \dfrac{{dW\left( t \right)}}{{dt}}\) |
| Kraft F | \(F = m \cdot a\) | \(F = \dfrac{{dW}}{{ds}}\) | |
| Arbeit | \(W = F \cdot s\) | \(W = \int {F\left( s \right)\,\,\operatorname{ds} }\) | |
| kinetische Energie Ekin | \({E_{kin}} = \dfrac{{m \cdot {v^2}}}{2}\) | ||
| potentielle Energie Epot | \({E_{pot}} = m \cdot g \cdot h\) | ||
| gleichförmige geradlinige Bewegung v(t) | \(v = \dfrac{s}{t}\) | \(v = \dfrac{{ds}}{{dt}}\) | \(v\left( t \right) = s'\left( t \right) = \dfrac{{ds}}{{dt}}\) |
| gleichmäßig beschleunigte geradlinige Bewegung a(t) | \(v = a \cdot t + {v_0}\) | \(a = \dfrac{{dv}}{{dt}}\) | \(a\left( t \right) = v'\left( t \right) = \dfrac{{dv}}{{dt}} = s''\left( t \right) = \dfrac{{{d^2}s}}{{d{t^2}}}\) |
Bewegungsvorgänge - Auswahl und Definition gemäß Formelsammlung BHS
| Größe | Formel |
| Zeit t | \(t\) |
| Weg-Zeit-Funktion s(t) | \(s\left( t \right) = \int {v\left( t \right)} \,\,dt\) |
| Geschwindigkeit-Zeit-Funktion v(t) | \(v(t) = s'\left( t \right) = \mathop s\limits^ \bullet = \dfrac{{ds}}{{dt}} = \int {a\left( t \right)} \,\,dt\) |
| Beschleunigung-Zeit-Funktion a(t) | \(a\left( t \right) = s''\left( t \right) = \mathop s\limits^{ \bullet \bullet } = \dfrac{{{d^2}s}}{{d{t^2}}} = v'\left( t \right) = \mathop v\limits^ \bullet = \dfrac{{dv}}{{dt}}\) |
Anmerkung zur auf Universitäten üblichen Kurzschreibweise von "Ableitungen nach der Zeit": Die Notation mit einem "Punkt" über dem Formelzeichen bedeutet, dass es sich um die 1 Ableitung nach der Zeit handelt. Zwei "Punkte" bedeuten, dass es sich um die 2. Ableitung nach der Zeit handelt.
Größen und ihre Einheiten - Auswahl gemäß Formelsammlung AHS
| Größe | Einheit | Symbol | Beziehung zu SI-Einheiten |
| Temperatur T | Grad Celsius Grad Kelvin |
°C K |
\(\Delta t = \Delta T\) |
| Frequenz f | Hertz | Hz | \(1 \cdot Hz = 1 \cdot {s^{ - 1}}\) |
| Arbeit W, Energie E, Wärmemenge Q | Joule | J | \(1 \cdot J = 1 \cdot kg \cdot {m^{2}}\cdot s^{ - 2}\) |
| Kraft F | Newton | N | \(1 \cdot N = 1 \cdot kg \cdot m \cdot {s^{ - 2}}\) |
| Drehmoment M | Newtonmeter | \(N \cdot m\) | \(1 \cdot N \cdot m = 1 \cdot kg \cdot {m^2} \cdot {s^{ - 2}}\) |
| Elektrischer Widerstand R | Ohm | \(\Omega\) | \(1 \cdot \Omega = 1 \cdot V \cdot {A^{ - 1}} = 1 \cdot kg \cdot {m^2} \cdot {A^{ - 2}} \cdot {s^{ - 3}}\) |
| Druck p | Pascal | Pa | \(1 \cdot Pa = 1 \cdot N \cdot {m^{ - 2}} = 1 \cdot kg \cdot {m^{ - 1}} \cdot {s^{ - 2}}\) |
| Elektrische Stromstärke I | Ampere | A | \(1 \cdot A = 1 \cdot C \cdot {s^{ - 1}}\) |
| Elektrische Spannung U | Volt | V | \(1 \cdot V = 1 \cdot J \cdot {C^{ - 1}} = 1 \cdot kg \cdot {m^2} \cdot {A^{ - 1}} \cdot {s^{ - 3}}\) |
| Leistung P | Watt | W | \(1 \cdot W = 1 \cdot J \cdot {s^{ - 1}} = 1 \cdot kg \cdot {m^2} \cdot {s^{ - 3}}\) |